11-11-2024 - Analytical Geometry - Linear Applications [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
11-11-2024 - Analytical Geometry - Linear Applications [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_081)
Linear Applications
Linear applications in analytical geometry are transformations between vector spaces that respect two fundamental properties. Below are explained what these two properties are.
-Linearity with respect to the sum
-Linearity with respect to the multiplication by a scalar
We can also say that a linear application transforms vectors into a vector space while maintaining the linear structure of this space. This means that linear applications between vector spaces do not generate curves or folds.
Formally we can say that an application T from a vector space V to a vector space W is linear if the additivity and homogeneity properties are verified.
Additivity property: T (u+v) = T(u) + T(v) for every pair of vectors u,v V
Homogeneity property: T (c v) = cT (v) for every vector v V and for every scalar c
Transformations that include linear applications are rotations, translations, homothetic transformations, reflections, cuts.
Exercise
Let's take a matrix A of dimensions 3 x 4, that is a matrix with 3 rows and 4 columns and let's try to understand what the domain is.
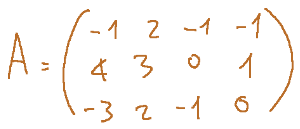
This matrix represents a linear application fA that maps vectors from a starting space to a target space. Now let's understand in two steps the domain and the codomain of fA considering the structure of the given matrix.
First step
The domain of a linear application defined by a matrix

is always

where n is the number of columns in the matrix.
Since matrix A has 4 columns, the domain of fA is R4. We can say that the application fa accepts R4 vectors as input (vectors with 4 components)
Second step
We start from the assumption that the codomain of fA is determined by the number of rows of the matrix. Since A has 3 rows, the codomain of fa is R3. So fa transforms a vector R4 into a vector R3
Result
The domain of fA is R4
Exercise 2
Always given the matrix A of dimensions 3 x 4 shown before and let's try to understand what the codomain is.
Let's repeat the matrix in question
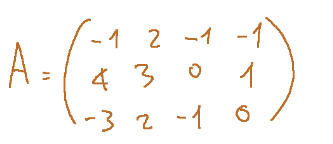
First step
Let's try to understand the meaning of the codomain of fa.
Basically for a linear application associated with a matrix

the codomain is determined by the number of rows of A. This is because each row represents a direction in the arrival space.
Second step
Now let's determine the codomain of fA.
Since the matrix A has 3 rows, the codomain fa is R3. This means that the linear application fa takes as input a vector R4 and produces as output a vector R3.
We can say that fa is a transformation that sends vectors from a 4-dimensional space (domain R4) to a 3-dimensional space (codomain R3)
The codomain is the target space that the linear application could theoretically cover, R3 in this case.
Result
The codomain of fA is
Conclusions
Linear applications are the maps between vector spaces that preserve the structure of the vector space.
Question
Have you ever heard of linear applications between vector spaces?

[ITALIAN]
11-11-2024 - Geometria analitica - Applicazioni lineari [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_081)
Applicazioni lineari
Le applicazioni lineari in geometria analitica sono trasformazioni tra spazi vettoriali che rispettano due proprietà fondamentali. Qui di seguito sono spiegate quali sono queste due proprietà.
-La linearità rispetto alla somma
-La linearità rispetto alla moltiplicazione per uno scalare
Possiamo anche dire che un’applicazione lineare trasforma vettori in uno spazio vettoriale mantenendo la struttura lineare di questo spazio. Questo significa che le applicazioni lineari tra spazi vettoriali non generano curve o piegature.
Formalmente possiamo dire che un’applicazione T da uno spazio vettoriale V a uno spazio vettoriale W è lineare se si verificano le proprietà di additività e di omogeneità.
Proprietà di additività: T (u+v) = T(u) + T(v) per ogni coppia di vettori u,v V
Proprietà di omogeneità: T (c v) = cT (v) per ogni vettore v V e per ogni scalare c
Le trasformazioni che includono le applicazioni lineari sono rotazioni, traslazioni, trasformazioni omotetie, riflessioni, tagli.
Esercizio
Prendiamo una matrice A di dimensioni 3 x 4, cioè una matrice con 3 righe e 4 colonne e cerchiamo di capire qual’è il dominio.
Esercizio
Prendiamo una matrice A di dimensioni 3 x 4, cioè una matrice con 3 righe e 4 colonne e cerchiamo di capire qual è il dominio.
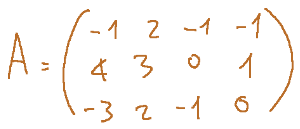
Questa matrice rappresenta un’applicazione lineare fA che mappa vettori da uno spazio di partenza ad uno spazio di arrivo. Ora cerchiamo di comprendere in due passi il dominio ed il codominio di fA considerando la struttura della matrice data.
Primo passo
Il dominio di un’applicazione lineare definita da una matrice

è sempre

dove n è il numero di colonne della matrice.
Poiché la matrice A ha 4 colonne, il dominio di fA è R4. Possiamo dire che l’applicazione fa accetta come input vettori R4 (vettori con 4 componenti)
Secondo passo
Partiamo dal presupposto che il codominio di fA è determinato dal numero di righe della matrice. Siccome A ha 3 righe, il codominio di fa è R3. Quindi fa trasforma un vettore R4 in un vettore R3
Risultato
Il dominio di fA è R4
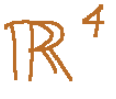
Esercizio 2
Data sempre la matrice A di dimensioni 3 x 4 mostrata prima e cerchiamo di capire qual è il codominio.
Ripetiamo la matrice in questione
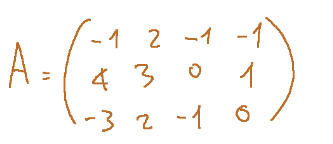
Primo passo
Cerchiamo di capire il significato del codominio di fa.
Sostanzialmente per un applicazione lineare associata a una matrice

il codominio è determinato dal numero di righe di A. Questo perché ogni riga rappresenta una direzione nello spazio di arrivo.
Secondo passo
Determiniamo ora il codominio di fA.
Siccome la matrice A ha 3 righe, il codominio fa è R3. Questo significa che l’applicazione lineare fa prende come input un vettore R4 e produce come output un vettore R3.
Possiamo dire che fa è una trasformazione che manda vettori da uno spazio a 4 dimensioni (dominio R4) a uno spazio a 3 dimensioni (codominio R3)
Il codominio è lo spazio di arrivo che l'applicazione lineare potrebbe teoricamente coprire, R3 in questo caso.
Risultato
Il codominio di fA è
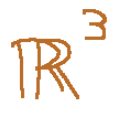
Conclusioni
Le applicazioni lineari sono le mappe tra spazi vettoriali che preservano la struttura di spazio vettoriale.
Domanda
Avete mai sentito parlare di applicazioni lineari tra spazi vettoriali?
THE END
I wish I was a science oriented person😅
This is a bit difficult
I confirm that I also think these are difficult things. Thanks for stopping by
Un argomento che abbiamo visto in università, in qualche modo lo utilizzo nel mio lavoro, quando consegno alcuni progetti.
Ti auguro un felice inizio settimana
Grazie per questa tua risposta. Questi argomenti per uno come me iniziano ad essere complicati, cioè, senza un ripasso non riesco mai a ricordarmeli bene.
!BEER
View or trade
BEER.Hey @stefano.massari, here is a little bit of
BEERfrom @thehockeyfan-at for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.!HOPE
!LOL
!INDEED
lolztoken.com
You need someone to fix their air conditioner.
Credit: reddit
@stefano.massari, I sent you an $LOLZ on behalf of cryptoyzzy
(6/10)
NEW: Join LOLZ's Daily Earn and Burn Contest and win $LOLZ
(1/5)
@stefano.massari! @cryptoyzzy Wants to spread Hope! so I just sent 1 HOP to your account on behalf of @cryptoyzzy.
Since we think the world can use more Hope, you can now already start spreading Hope yourself!
(6/10)
@stefano.massari! @cryptoyzzy Totally agrees with your content! so I just sent 1 IDD to your account on behalf of @cryptoyzzy.