28-11-2024 - Analytic Geometry - Quadratic Forms [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
28-11-2024 - Analytic Geometry - Quadratic Forms [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_62)

Quadratic Forms
Quadratic forms, which are a generalization
of the norms.

that is

is a polynomial with only monomials of degree 2, or the null polynomial

Remark
For every quadratic form we have

Example
The polynomial

with

defines a quadratic form. The associated matrix is ​​the matrix

Example 2
Let's try to find the associated matrix of the following quadratic form
Q(X) = 3X^2 + 2Y^2 in R3

Let's proceed by writing the quadratic form in matrix terms as follows:

where V is equal to a

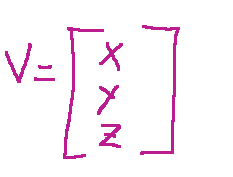
and is the variable vector and A is an associated symmetric matrix.

2-
The matrix A contains the coefficients of the quadratic and mixed terms. In this case there are no mixed terms (like XT, XZ, YZ), so A will be diagonal.
3-
The given quadratic form is the following

this implies the fact that
-The coefficient of x^2 is 3
-The coefficient of y^2 is 2
-The coefficient of z^2 is 0

4-
The matrix will therefore be the following:

Result
The matrix associated with the form quadratic

is

Conclusions
Quadratic matrices find application in various fields, from the classification of conics and quadrics to the description of geometric transformations.

Question
Have you ever tried to do exercises with quadratic matrices? In my opinion they are a bit complex, and in your opinion?

---

---

[ITALIAN]
28-11-2024 - Geometria analitica - Forme quadratiche [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_62)

Forme quadratiche
Le forme quadratiche, che sono una generalizzazione
delle norme.

ossia

è un polinomio con solo monomi di grado 2, o il polinomio nullo

Osservazione
Per ogni forma quadratica abbiamo

Esempio
Il polinomio

con

definisce una forma quadratica. La matrice associata è la matrice

Esempio 2
Proviamo a trovare la matrice associata della seguente forma quadratica
Q(X) = 3X^2 + 2Y^2 in R3

Procediamo scrivendo la forma quadratica in termini matriciali come segue:

dove V è uguale a

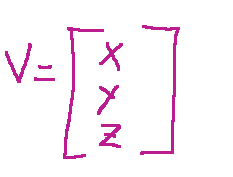
ed è il vettore variabile e A è una matrice simmetrica associata.

2-
La matrice A contiene i coefficienti dei termini quadratici e misti. In questo caso non ci sono termini misti (come XT, XZ, YZ), quindi A sarà diagonale.
3-
La forma quadratica data è la seguente

questo implica il fatto che
-Il coefficiente di x^2 è 3
-Il coefficiente di y^2 è 2
-Il coefficiente di z^2 è 0

4-
La matrice quindi sarà la seguente:

Risultato
La matrice associata alla forma quadratica

è

Conclusioni
Le matrici quadratiche trovano applicazione in diversi ambiti, dalla classificazione delle coniche e delle quadriche alla descrizione di trasformazioni geometriche.

Domanda
Avete mai provato a fare degli esercizi con le matrici quadratiche? Secondo me sono un po' complessi, e secondo voi?

THE END