26-11-2024 - Analytic Geometry - Orthonormal Bases [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
26-11-2024 - Analytic Geometry - Orthonormal Bases [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_64)

Orthonormal Bases and Vector Product
An orthonormal basis is a set of vectors that satisfies two main properties, orthogonality and normalization.
-Orthogonality means that the vectors of the basis are orthogonal in pairs.
This means that the scalar product between two distinct vectors of the basis is zero.

-Normalization means that each vector in the basis has a unit norm, that is:

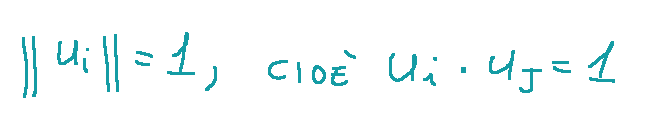
An orthonormal basis is useful because it simplifies calculations. For example, the coordinates of a vector with respect to an orthonormal basis can be computed directly as scalar products:

Example
The canonical basis of the R3 space is as follows:

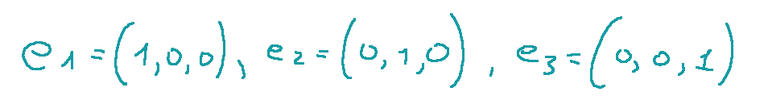
The vector product
First of all we must understand that in this case we are in a three-dimensional space. So the vector product is an operation defined in R3 that associates to two vectors u and v a third vector w = u x v, which satisfies the properties of orthogonality, modulus and direction.

Explicit formula
Given u = (u1,u2,u3) and v =(v1,v2,v3) the vector product will be the following:

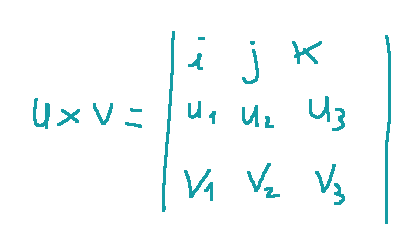
where i, j, k are the vectors of the canonical basis R3.

Gram–Schmidt orthonormalization process applied to vectors
The Gram-Schmidt orthonormalization process is a method used to transform a set of linearly independent vectors into an orthonormal one (a set of vectors that are orthogonal to each other and have unit norm).
The method consists of three main steps:
-First step: normalize the first vector
-Second step: orthogonalize the second vector
-Third step: identify the vector v with the normalization applied in the last transformation.

Example

Let's try to find the vector components and scalar components of the geometric vector (3 -1 0) with respect to the orthonormal basis { i, j, k }

We can immediately make a consideration that the standard basis (i, j, k) is already an orthonormal basis where:
i = (1,0,0), j = (0,1,0), k = (0,0,1)

1-Scalar components
The scalar components of v are directly its values ​​along each axis of the basis, therefore:
Scalar components = (3, -1, 0)
This means that the component along i is 3, the component along j is -1 and the component along k is 0.
2-Vector components
The vector components are obtained by multiplying each scalar component by the corresponding basis vector, here below i steps:

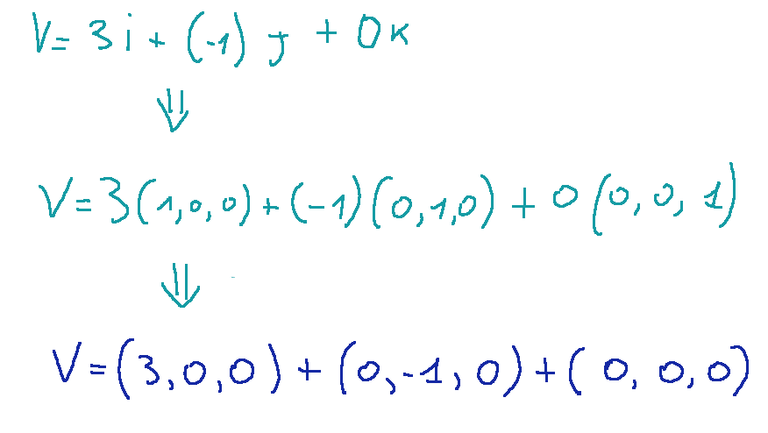
Result
-Scalar components: (3, -1, 0)
-Vector components:

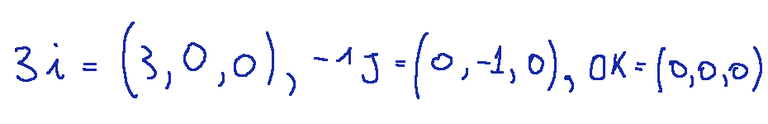
shown as column vectors would be the following

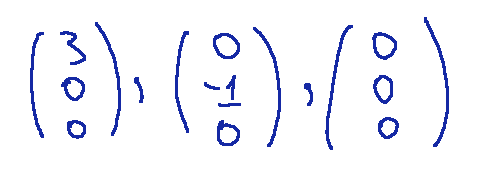
The reconstruction of v from the basis is:

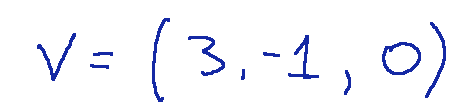
Conclusions
Orthonormal bases are used in the representation of rotations and linear transformations.
The vector product is fundamental in physics to calculate moments, torques and the description of phenomena such as the magnetic field.

Question
Have you studied the orthonormal bases and the vector product in analytical geometry?

---

---

[ITALIAN]
26-11-2024 - Geometria analitica - Basi ortonormali [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_64)

Basi ortonormali e prodotto vettoriale
Una base ortonormale è un insieme di vettori che soddisfa due proprietà principali, l’ortogonalità e la normalizzazione.
-L’ortogonalità significa che i vettori della base sono a due a due ortogonali.
Questo significa che il prodotto scalare tra due vettori distinti della base è zero.

-La normalizzazione significa che ogni vettore della base ha norma unitaria, cioè:

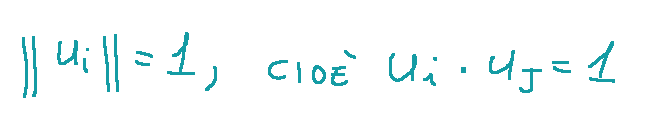
Una base ortonormale è utile perché semplifica i calcoli. Ad esempio, le coordinate di un vettore rispetto a una base ortonormale possono essere calcolate direttamente come prodotti scalari:

Esempio
La base canonica dello spazio R3 è la seguente:

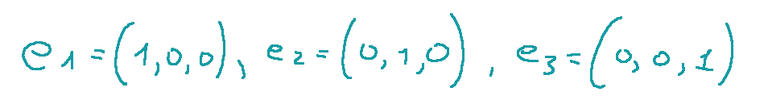
Il prodotto vettoriale
Prima di tutto dobbiamo comprendere che in questo caso siamo in uno spazio tridimensionale. Quindi il prodotto vettoriale è un'operazione definita in R3 che associa a due vettori u e v un terzo vettore w = u x v, il quale soddisfa le proprietà di ortogonalità, di modulo e di direzione.

Formula esplicita
Dato u = (u1,u2,u3) e v =(v1,v2,v3) il prodotto vettoriale sarà il seguente:

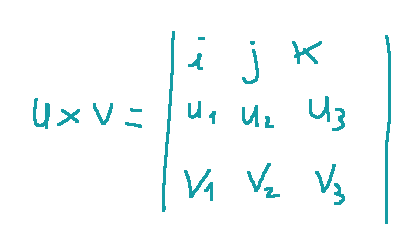
dove i, j, k sono i vettori della base canonica R3.

Processo di ortonormalizzazione di Gram–Schmidt applicato ai vettori
Il processo di ortonormalizzazione di Gram-Schmidt è un metodo utilizzato per trasformare un insieme di vettori linearmente indipendenti in uno ortonormale (un insieme di vettori che sono ortogonali tra loro e hanno norma unitaria).
Il metodo consiste in tre passi principali:
-Primo passo: normalizzare il primo vettore
-Secondo passo: ortogonalizzare il secondo vettore
-Terzo passo: identificare il vettore v con la normalizzazione applicata nell’ultima trasformazione.

Esempio

Proviamo a trovare le componenti vettoriali e le componenti scalari del vettore geometrico (3 -1 0) rispetto alla base ortonormale { i, j, k }

Possiamo fare subito una considerazione che la base standard (i, j, k) è già una base ortonormale dove:
i = (1,0,0), j = (0,1,0), k = (0,0,1)

1-Componenti scalari
Le componenti scalari di v sono direttamente i suoi valori lungo ciascun asse della base, quindi:
Componenti scalari = (3, -1, 0)
Questo significa che la componente lungo la i è 3, la componente lungo j è -1 e la componente lungo k è 0.
2-Componenti vettoriali
Le componenti vettoriali sono ottenute moltiplicando ciascuna componente scalare per il corrispondente vettore base, qui di seguito i passaggi:

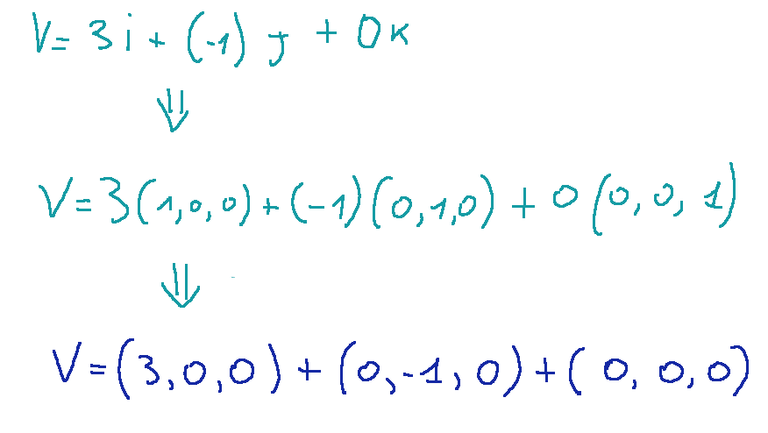
Risultato
-Componenti scalari: (3, -1, 0)
-Componenti vettoriali:

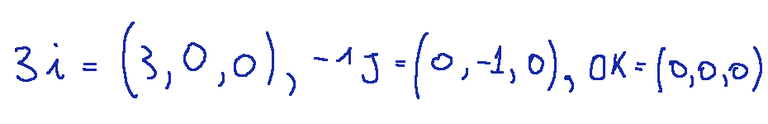
mostrati come vettori colonna sarebbero i seguenti

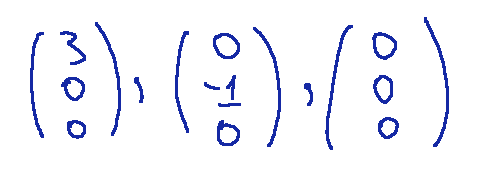
La ricostruzione di v dalla base è:

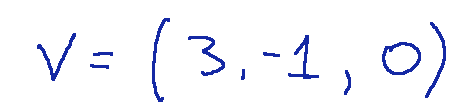
Conclusioni
Le basi ortonormali vengono usate nella rappresentazione di rotazioni e trasformazioni lineari.
Il prodotto vettoriale è fondamentale in fisica per calcolare momenti, forze torcenti e la descrizione di fenomeni come il campo magnetico.

Domanda
Avete studiato in geometria analitica le basi ortonormali e il prodotto vettoriale?

THE END