17-11-2024 - Analytic Geometry - Existence and Uniqueness of Solutions [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
17-11-2024 - Analytic Geometry - Existence and Uniqueness of Solutions [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_75)

Existence and Uniqueness of Solutions
Description
When we talk about systems of linear equations through matrices we can study the existence of solutions.
We can first name the Rouché-Capelli theorem).
This theorem states that a system of linear equations A * X = B is compatible if the incomplete matrix and the complete matrix have the same rank.
We can describe it as follows

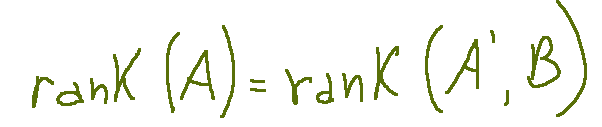
Example
Consider the following real system of linear equations.

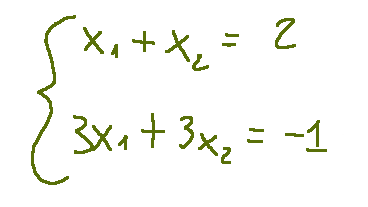
The rank of the incomplete matrix, i.e. the following…

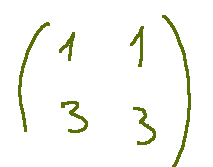
… is 1, while the rank of the incomplete matrix …

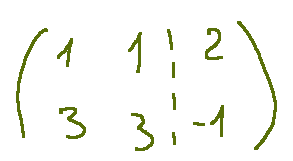
… is 2
so the system of linear equations is not compatible.

Example
Let's consider the following linear equation:

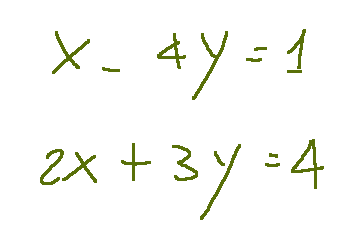
Let's try to understand if this linear equation has a solution.
We must now verify that the determinant of the coefficient matrix is ​​not zero. If the determinant is different from zero, the system is determined and has only one solution.

Let's reconstruct the coefficient matrix

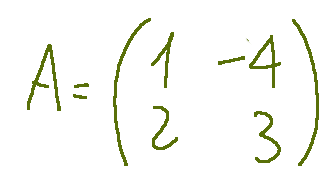
Determinant
The determinant of A is calculated in the following way

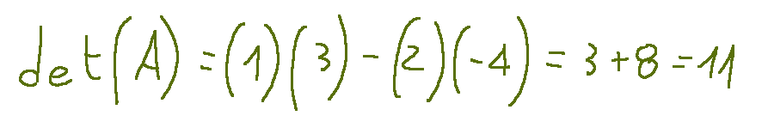
Result
Since the determinant det(A) = 11, therefore different from zero, the system has only one solution.

Conclusions
When we study systems of linear equations through some methods we can immediately understand, before performing complex calculations, if the equation has a solution.

Question
Have you ever heard of the Rouché-Capelli theorem related to systems of linear equations?

---

---

[ITALIAN]
17-11-2024 - Geometria analitica - Esistenza e unicità delle soluzioni [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_75)

Esistenza e unicità delle soluzioni
Descrizione
Quando parliamo di sistemi di equazioni lineari attraverso le matrici possiamo studiare l’esistenza delle soluzioni.
Possiamo nominare per prima cosa il teorema di Rouché-Capelli).
Questo teorema afferma che un sistema di equazioni lineari A * X = B è compatibile se la matrice incompleta e la matrice completa hanno lo stesso rango.
Possiamo descrivere la cosa come segue

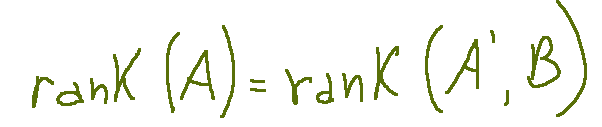
Esempio
Consideriamo il seguente sistema di equazioni lineari reale.

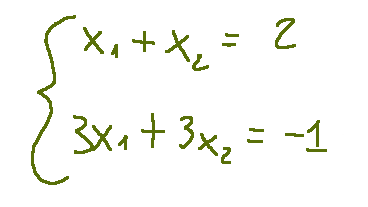
Il rango della matrice incompleta, cioè la seguente…

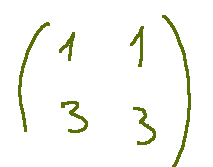
… è 1, mentre il rango della matrice incompleta …

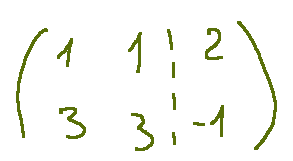
… è 2
quindi il sistema di equazioni lineari non è compatibile.

Esempio
Prendiamo in considerazione la seguente equazione lineare:

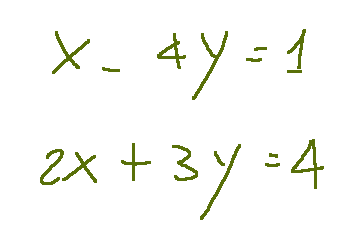
Proviamo a capire se questa equazione lineare ha una soluzione.
Dobbiamo ora verificare che il determinante della matrice dei coefficienti non sia zero. Se il determinante è diverso da zero, il sistema è determinato e ha una sola soluzione.

Ricostruiamo la matrice dei coefficienti

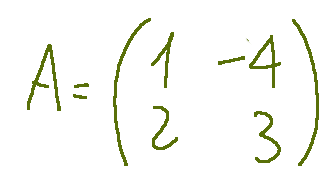
Determinante
Il determinante di A è calcolato nella seguente maniera

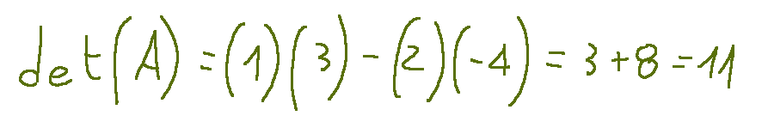
Risultato
Siccome il determinante det(A) = 11, quindi diverso da zero, il sistema ha una sola soluzione.

Conclusioni
Quando studiamo sistemi di equazioni lineari attraverso alcuni metodi possiamo capire subito, prima di eseguire calcoli complessi se l'equazione ha una soluzione.

Domanda
Avete mai sentito parlare del teorema di Rouché-Capelli legato ai sistemi di equazioni lineari?

THE END