09-12-2024 - Computer science basics - Conversion rules [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
09-12-2024 - Computer science basics - Conversion rules [EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_96)

Conversion rules
First rule
To switch from the binary system to the decimal system you can use conversion rules.
The positional system allows you to convert a number from a binary coding system to a number in the decimal system. This observation also applies to octal and hexadecimal encodings. In fact, using the same criterion, it is possible to convert an octal and/or hexadecimal number into a decimal number.

First conversion rule (from base b to base 10)
In general, given a generic base b and the number ap ap-1 ap-2… a1 a0 (where ap, ap-1, ap-2, a1 and a0 are the digits that make up the number in base b), to convert this number to decimal base (N10) the formulation is as follows:

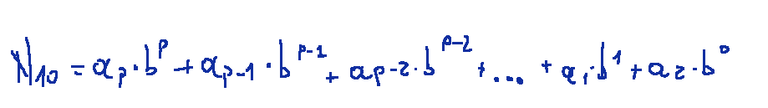
Second conversion rule
Second conversion rule (from base 10 to base b)
The second conversion rule concerns the opposite conversion: from number N in base 10 to number in base b.
This rule consists of the following steps:
⎯ Repeated divisions of the number N by the value of the base b
⎯ Each single i-th remainder of the division represents a digit of the number in base b (starting from the least significant digit)
⎯ The quotient of the division becomes the new dividend of the next division
⎯ The cycle repeats until the last quotient becomes zero.
Example 2 below explains this rule.

Example 01
What number in decimal corresponds to the number 123 in octal?

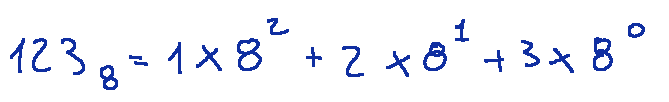
Below with purple and light blue I have marked the correspondences:

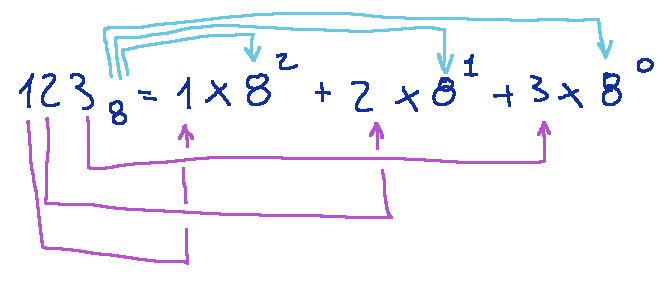
Below the calculation

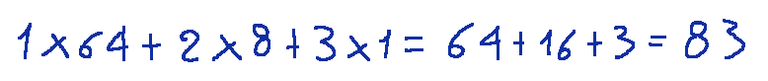
Example 02
What binary number corresponds to the number 611 in decimal?
611÷2=305 remainder1
305÷2=152 remainder1
152÷2=76 remainder0
76÷2=38 remainder0
38÷2=19 remainder0
19÷2=9 remainder1
9÷2=4 remainder1
4÷2=2 remainder0
2÷2=1 remainder0
1÷2=0 remainder1

Result
611 (decimal) = 1001100011 (binary)

Conclusions
Conversion rules in computer science are used to translate data from one representation system to another. This is essential because computers process information in binary formats, while humans use systems such as decimal, hexadecimal, octal, and others.

Question
Do you remember applying these conversion rules at school? Have you ever tried to convert decimal numbers into binary numbers or vice versa?

---

---

[ITALIAN]
09-12-2024 - Basi di informatica - Regole di conversione [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_96)

Regole di conversione
Prima regola
Per passare dal sistema binario al sistema decimale si possono usare delle regole di conversione.
Il sistema posizionale consente di convertire un numero da un sistema di codifica binario ad un numero nel sistema decimale. Quest’osservazione vale anche per le codifiche ottale ed esadecimale. Utilizzando lo stesso criterio, infatti, è possibile convertire un numero ottale e/o esadecimale in un numero decimale.

Prima regola di conversione (da base b a base 10)
In generale, data una base generica b e il numero ap ap-1 ap-2… a1 a0 (dove ap, ap-1, ap-2, a1 e a0 sono le cifre che compongono il numero in base b), per convertire tale numero in base decimale (N10) la formulazione è la seguente:

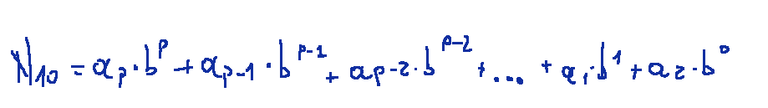
Seconda regola di conversione
Seconda regola di conversione (da base 10 a base b)
La seconda regola di conversione riguarda la conversione opposta: da numero N in base 10 a numero in base b.
Tale regola si compone dei seguenti step:
⎯ Divisioni ripetute del numero N per il valore della base b
⎯ Ogni singolo resto i-esimo della divisione rappresenta una cifra del numero in base b (a partire dalla cifra meno significativa)
⎯ Il quoziente della divisione diventa il nuovo dividendo della divisione successiva
⎯ Il ciclo si ripete fin quando l’ultimo quoziente diventa zero.
L'esempio 2 qui di seguito proposto spiega questa regola.

Esempio 01
A quale numero in decimale corrisponde il numero 123 in ottale?

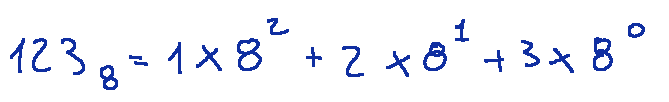
Qui di seguito con il viola e l'azzurro ho segnalato le corrispondenze:

Qui di seguito il calcolo

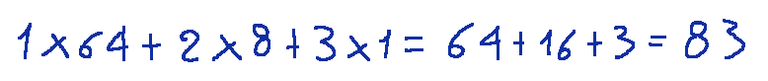
Esempio 02
A quale numero binario corrisponde il numero 611 in decimale?
611÷2=305 resto 1
305÷2=152 resto 1
152÷2=76 resto 0
76÷2=38 resto 0
38÷2=19 resto 0
19÷2=9 resto 1
9÷2=4 resto 1
4÷2=2 resto 0
2÷2=1 resto 0
1÷2=0 resto 1

Risultato
611 (decimale) = 1001100011 (binario)

Conclusioni
Le regole di conversione in informatica servono a tradurre i dati da un sistema di rappresentazione a un altro. Questo è fondamentale perché i computer elaborano informazioni in formati binari, mentre gli esseri umani utilizzano sistemi come il decimale, esadecimale, ottale, e altri.

Domanda
Ricordate di aver applicato a scuola queste regole di conversione? Avete mai provato a convertire dei numeri decimali in numeri binari o viceversa?

THE END