Perfección matemática en las plantas (Esp/Eng)

La primera vez que observé el interior de las plantas a través de los lentes de aumento de un microscopio de luz, se me abrió un mundo maravilloso y no volví a ver a las plantas de otra manera que no fuera con admiración.
La perfección de sus células ordenadas en filas cada una para cumplir una función específica, como se comunican entre ellas a través de los plasmodesmos, delgados hilos de protoplasma que atraviesan las paredes celulares. Y cómo estos tejidos fundamentales se continúan desde la raíz hasta el tallo y en cada rama, hoja y flor y se disponen de acuerdo a la morfología del órgano y, por supuesto, a su función.
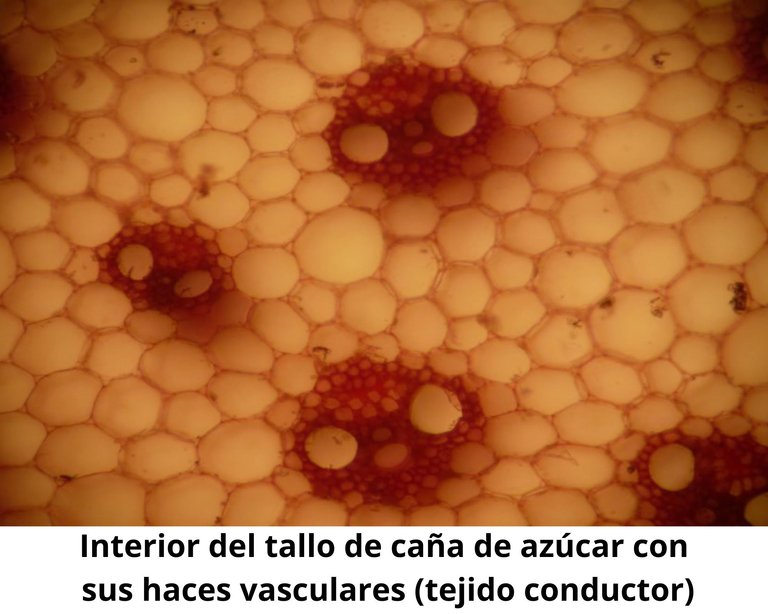
Desde una disposición radial en la raíz y tallo hasta la ubicación dorsiventral en las hojas, todo se ajusta perfectamente. Allí nada está de más, a no ser que un invasor como un hongo, bacteria o virus penetre sus tejidos y ocasione modificaciones.
Consideramos a las matemáticas como la ciencia de la exactitud. La numeración arábiga que fue difundida por los árabes, aunque se cree es de origen fenicio, que era usada para contar la mercancía en transacciones comerciales, contribuyo a abrir un gran portal de comprensión de los fenómenos naturales que solo podían ser observados y comparados de forma cualitativa.
Las mediciones permitieron comparar y establecer diferencias y similitudes y aún más, el diseño de fórmulas para expresar fenómenos, como por ejemplo las ecuaciones que tratan de explicar los procesos de desarrollo animal, como las elaboradas por el matemático inglés Alan Turing, para explicar los patrones de pigmentación en los animales.
Alan Turing, recordado por su decisiva actuación descifrando códigos nazis durante la Segunda Guerra Mundial, también se interesó por la biología y en uno de sus últimos trabajos “La base química de la morfogénesis”, estudio cómo aparecen estructuras y formas (o "patrones") de manera "espontánea" en distintos sistemas físicos, químicos y biológicos.
Es aquí donde las matemáticas nos hablan de coincidencias entre organismos vegetales y animales, asombrosos diseños de sus cuerpos con las mismas proporciones geométricas. Un ejemplo de esto es el número aureo.
Los espirales del caracol son un ejemplo de este diseño.
 @popurri
@popurriQue es el número áureo o número de oro
El número áureo es un número irracional, porque no es entero y sus decimales son infinitos. ¿Por qué es tan interesante este número, si pareciera que es solo uno entre tantos otros y no es más que la proporción geométrica entre dos líneas rectas?
Se ha determinado que esta relación geométrica se mantiene en el desarrollo de ciertas estructuras vegetales y animales con una perfección que es asombrosa.
Benoît Mandelbrot, un matemático polaco, explicó en su libro Fractales, formas, azar y dimensión (1977) la frecuencia de la geometría fractal en la naturaleza. Este autor decía que muchas de las formas encontradas en la naturaleza podían ser descritas mediante formas matemáticas, llamadas fractales.
 @popurri
@popurriBasado en el trabajo previo del matemático francés Gastón Julia (1893-1978), los llamados Conjuntos de Julia, el mismo autor en su libro, Geometría fractal de la naturaleza (1982), señala
"Las nubes no son esferas, las montañas no son conos, las costas no son círculos, como la corteza de un árbol no es plana ni un rayo viaja en línea recta… La naturaleza no solamente exhibe un grado mayor, sino también un nivel diferente de complejidad".
Muchos de los sistemas de ramificación de las plantas siguen una distribución fractal, como el de esta inflorecencia de Bohemeria.
 @popurri
@popurri¿Qué es un fractal?
"Un fractal se define como un objeto geométrico que posee una estructura repetitiva. Aparentemente, es irregular o fragmentado, pero en realidad expresa un orden recurrente que se manifiesta en diferentes niveles de complejidad en la naturaleza"
Para entenderlo mejor, los fractales tienen la propiedad de la autosimilitud, es decir, una figura geométrica es autosímil si al ver una de sus partes con lupa, reconocemos la forma de toda la figura de nuevo. Se puede decir que va reduciendo su tamaño.
Mandelbrock y otros investigadores relacionaron estas expresiones geométricas con el diseño de la naturaleza. ¿Qué observaciones realizaron?, ¿Cuáles fueron sus pensamientos para llegar a relacionar una proporción matemática con los organismos vivos? Se puede decir que fue un destello de comprensión, una intuición que los llevó a estudiar este diseño en múltiples formas.
Si vemos una planta, su forma externa e interna es el resultado de un proceso de desarrollo que se inicia con la unión de dos gametas, masculina y femenina, al igual que los animales en donde nos incluimos y también en otros organismos pluricelulares.
 @popurri
@popurriEl desarrollo del embrión se inicia por procesos de división celular donde el número de células aumenta exponencialmente, mientras que también ocurren procesos de diferenciación celular, es decir, células que eran idénticas comienzan a cambiar y al unirse forman los diferentes tejidos y órganos. Cada uno de estos cumplirá una función específica en el individuo completo, sea planta o animal
Pero en las plantas, a diferencia de los animales, el proceso de crecimiento y diferenciación continúa durante su ciclo de vida con la formación de nuevos tejidos y órganos a través de los ápices o puntos de crecimiento. Es el tejido meristemático que tiene esta función, como se produce en las hojas de Kalanchoe.
 @popurri
@popurriPor fuera vemos la forma de la planta, la morfología y por dentro su estructura, su anatomía, los tejidos que la definen cada uno con una función específica.
El desarrollo de las hojas a lo largo del eje del tallo o filotaxis es un ejemplo de la precisión matemática que puede observarse en las plantas. En término más amplio, no solo hace referencia a las hojas, sino también a las ramas, flores y semillas.
 @popurri
@popurriLa filotaxis está determinada por el número de elementos en cada nudo del tallo y el ángulo de divergencia entre dos nudos consecutivos. Y he aquí que existe una filotaxis en espiral cuyo ángulo está determinado por la proporción áurea que es cerca de 137.5 °.
El ejemplo más famoso es la cabeza de girasol. Este patrón filotáctico crea un efecto óptico de espirales entrecruzadas. Esta distribución tiene una razón de ser y es una mayor eficiencia en la distribución de la semillas de girasol.

Este patrón se encuentra en un gran número de especies de plantas y obedece a un orden específico que garantiza la supervivencia.
En las plantas observamos una maravillosa complejidad con diferencias entre grupos de órdenes, clases, familias y géneros; sin embargo, exhibe ciertas similitudes que las matemáticas han ayudado a identificar y algunas de estas similitudes también se encuentran en otros seres vivos, es como una marca, un patrón fractal que se repite en la naturaleza.
¿Pudiéramos pensar que estos patrones tienen un significado más allá del de la funcionalidad de los seres vivos? La naturaleza está llena de maravillosos y múltiples ejemplos de estos diseños matemáticos que están presentes en todo el asombroso mundo en el que vivimos.
 @popurri
@popurri

The first time I observed the interior of plants through the magnifying lenses of a light microscope, a wonderful world opened up to me and I never saw plants in any other way than with admiration.
The perfection of their cells arranged in rows each one to fulfill a specific function, how they communicate with each other through plasmodesmata, thin threads of protoplasm that cross the cell walls. And how these fundamental tissues continue from the root to the stem and in each branch, leaf and flower and are arranged according to the morphology of the organ and of course to its function.
From a radial disposition in the root and stem to the dorsiventral location in the leaves, everything fits perfectly, there is nothing in excess, unless an invader such as a fungus, bacteria or virus penetrates its tissues and causes modifications.
We consider mathematics as the science of accuracy. Larabic numeration, which was spread by the Arabs, although it is believed to be of Phoenician origin, was used to count merchandise and in commercial transactions and contributed to open a great portal of understanding of natural phenomena that could only be observed and compared qualitatively.
Measurements made it possible to compare and establish differences and similarities, and furthermore, the design of formulas to express phenomena, such as equations that try to explain animal development processes, as well as the development of the equations that explain the processes of animal development, as well as the development of the equations that explain the processes of animal development, as well as the development of the equations that explain animal development.
The first of these was the work developed by the English mathematician Alan Turing, to explain the pigmentation patterns in animals.
Alan Turing, remembered for his decisive action in deciphering Nazi codes during the Second World War, was also interested in biology and in one of his last works "The chemical basis of morphogenesis", he studied how structures and forms (or "patterns") appear "spontaneously" in different physical, chemical and biological systems.
It is here that mathematics tells us about coincidences between plant and animal organisms, amazing designs of their bodies with the same geometric proportions. An example is the golden number.
The spirals of the snail are an example of this design.
 @popurri
@popurriThe golden ratio or golden number
The golden number is an irrational number, because it is not integer and its decimals are infinite. Why is this number so interesting, if it seems that it is only one among many others and it is nothing more than the geometric proportion between two straight lines?
It has been determined that this geometric relationship is maintained in the development of certain plant and animal structures with a perfection that is astonishing.
Benoit Mandelbrot, a Polish mathematician, explained in his book Fractals, shapes, randomness and dimension (1977) the frequency of fractal geometry in nature. This author said that many of the shapes found in nature could be described by mathematical forms, called fractals.
Based on the earlier work of the French mathematician Gaston Julia (1893-1978), the so-called the so-called Julia Sets, the same author in his book, Fractal Geometry of Nature (1982), states.
"Clouds are not spheres, mountains are not cones, coastlines are not circles, just as the bark of a tree is not flat nor does lightning travel in a straight line... Nature exhibits not only a greater degree but also a different level of complexity".
Many of the branching systems of plants follow a fractal distribution.
 @popurri
@popurriWhat is a fractal?
"A fractal is defined as a geometric object that possesses a repetitive structure. It is apparently irregular or fragmented, but in reality it expresses a recurring order that manifests itself at different levels of complexity in nature"
To understand it better, they have the property of self-similarity, that is to say, a geometric figure is self-similar, if when we see one of its parts with a magnifying glass we recognize the shape of the whole figure again. It can be said that it is reducing its size.
Mandelbrock and other researchers related these geometrical expressions to the design of nature, what observations did they make, what were their thoughts that led them to relate a mathematical proportion to living organisms? A flash of understanding, an intuition that led them to study this design in multiple forms.
If we look at a plant, its external and internal form is the result of a development process that begins with the union of two gametes, male and female, just like the animals in which we are included and also in other multicellular organisms.
The development of the embryo is initiated by cell division processes where the number of cells increases exponentially, while cell differentiation processes also occur, i.e. cells that were identical begin to change and when they unite they form the different tissues and organs. Each of these will fulfill a specific function in the complete individual, be it plant or animal.
 @popurri
@popurriBut in plants, unlike animals, the process of growth and differentiation continues during their life cycle with the formation of new tissues and organs through the apices or growing points. It is the meristematic tissue that has this function. As it occurs in the leaves of Kalanchoe.
 @popurri
@popurriOn the outside we see the shape of the plant, the morphology and inside its structure, its anatomy, the tissues that define it, each with a specific function.
The development of the leaves along the axis of the stem or phyllotaxis is an example of the mathematical precision that can be observed in plants. In a broader term it refers not only to the leaves, but also to the branches, flowers and seeds.
 @popurri
@popurriThe phyllotaxis is determined by the number of elements in each node and the angle of divergence between two consecutive nodes. And here is that there is a spiral phyllotaxis whose angle is determined by the golden ratio which is about 137.5 °.
The most famous example is the sunflower head. This phyllotactic pattern creates an optical effect of crisscrossing spirals. This distribution has a raison d'être and is a greater efficiency in the distribution of the sunflower seed.

This pattern is found in a large number of plant species and obeys a specific order that guarantees survival.
In plants we observe a wonderful complexity with differences between groups of orders, classes, families and genera, however it exhibits certain similarities that mathematics has helped to identify and some of these similarities are also found in other living beings, it is like a mark, a fractal pattern that is repeated in nature.
Could we think that these patterns have a meaning beyond the functionality of living things? Nature is full of wonderful and multiple examples of these mathematical designs, they are present all over the amazing world we live in.

Referencias consultadas
https://www.cairn.info/revue-recherches-en-sciences-de-gestion-2012-3-page-43.htm
https://www.nationalgeographic.com.es/ciencia/fractales-patrones-que-se-encuentran-naturaleza_20807
https://nadaesgratis.es/anxo-sanchez/turing-y-sus-patrones-el-pionero-de-la-biologia-matematica
https://es.wikibrief.org/wiki/Phyllotaxis
https://mahtblog.wordpress.com/2011/09/06/filotaxis-espiral-vs-angulo-dorado/

La traducción sl inglés la realicé en www.deepl.com
La imágen de la presentación la edité en Canva con una fotografía propia.
Todas las fotografías son de mi autoría
Muy buen trabajo de divulgación científica de ese fenómeno extraordinario que conocemos como fractal. Desde que supe de él, hace muchos años, me pareció casi una aplicación poética al mundo de las ciencias; en la heráldica o la literatura, algo muy parecido a la "puesta en abismo" ("mise en abîme"). Gracias, @popurri.
PD: ¿Académicamente, vienes del campo de las ciencias duras, como le dicen, o de las ciencias naturales?
Me agrado mucho leer tu comentario @josemalavem. Te lo agradezco. Los fractales son un fenómeno asombroso e interesante y como tu dices es un arte en la naturaleza. Que bonito simil. Tuve que buscar el significado de "puesta en abismo" para entenderlo.
Mi formación es en ciencias naturales porque estudie agronomia y trabaje muchos años en investigación agrícola. Pero mi admiracion por las plantas va mas allá de su utilidad para el hombre. Son seres vivos maravillosos.
Saludos y feliz tarde 🌻
¡Felicidades! Esta publicación obtuvo upvote y fue compartido por @la-colmena, un proyecto de Curación Manual para la comunidad hispana de Hive que cuenta con el respaldo de @curie.
Si te gusta el trabajo que hacemos, te invitamos a darle tu voto a este comentario y a votar como testigo por La Colmena.
Si quieres saber más sobre nuestro proyecto, te invitamos a acompañarnos en nuestro servidor de Discord.
Muchas gracias @la-colmena, por el apoyo a mi publicación. Es un gran estimulo para continuar escribiendo sobre estos temas.
Saludos 🌼
No conocía estos estudios aunque si había observado en mis flores de girasol un equilibrio perfecto a la vista. Muy interesante recorrido en los aspectos a observar. Un abrazo.
Muchas gracias querida @sacra97.
Esta información es muy interesante, las plantas son seres maravillosos. Me alegra que te haya gustado.
Un abrazo