This time a tricky one based on a circle and its tangent & secant

Helloo! math bugs(🐞) and hivers(🐝)
I hope you are strong and stout & doing great in life.

Well come to another new problem and its solution. First let me explain the question a little bit; otherwise you may have problem to undersatnd the data given in cover figure. There is a given circle. AB is its one tangent and BD is a secant touches the circumference at B and C. ∠ABD = 50° and ∠BAD = 80°. Thought may come in your head that AB is diameter. For your kind information, it is not actually.

I'll ask you to give it a try first and you may drop your answer in comment section. If you find difficulty to sovle it, go ahead to the solution.

Before heading towards solution, I just want to mention the concepts/thoughts/axioms/postulates we gonna need to solve it.

1️⃣ Relation of a tangent and a secant of a circle. For details check my previous post. You must find relation of two secant there. Incase of tangent it, will be sqaure of tangent is equals to product the secant and outer line segment. According to the problem we can say AD² = BD×CD. So, Now we can find lentgh of BC.

2️⃣ Secondly, we need to know angle in alternate segment. If a triangle is drawn inside a circle and one of its vertex is at the point of contact of a tangent of the dame cirlce, the angles made by sides of the trinage and the tangent are equal to the angle opposite to it. You may be confused or my words aren't enough to make you understand. You better check details here.

3️⃣ On the same arc of a circle, the angle on the opposite arc is half the angle on the cir-cum-centre. All are hidden in this figure we gonna draw it in a bit but before that you can check details here.

4️⃣ If two angles of a triangle are equal, the opposite side is also equal and if three angles of triangle equals, it becomes a eqilateral triangle. Hence lenth of each side will be the same.

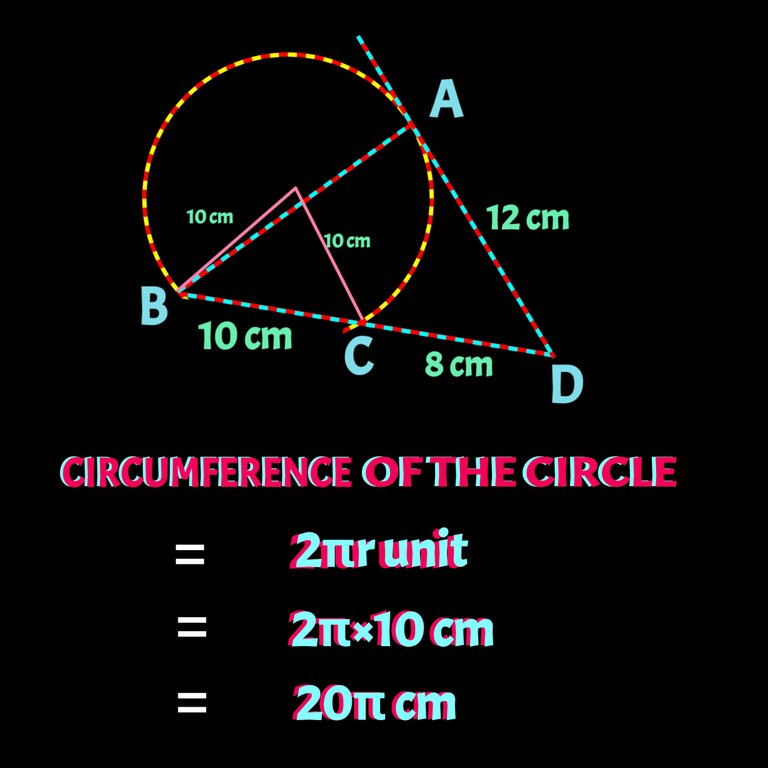
5️⃣ Circumference of a circle is given by 2πr unit where r is the raius of a circle.

If you got these 5 pints, you are pretty much okay to deal with the problem. If you want, you can give it a try now.

SOLUTION:

If we draw AC, let's see what we can have then. Check below angles in alternative segment are equal as I mentioned in point 2️⃣.

It was given that ∠BAD = 80° and we got ∠CAD = 50°. Hence ∠BAC = (80°-50°) = 30°. Now it's time to draw the circumcentre, I mentioned in point 3️⃣ Check it below.👇

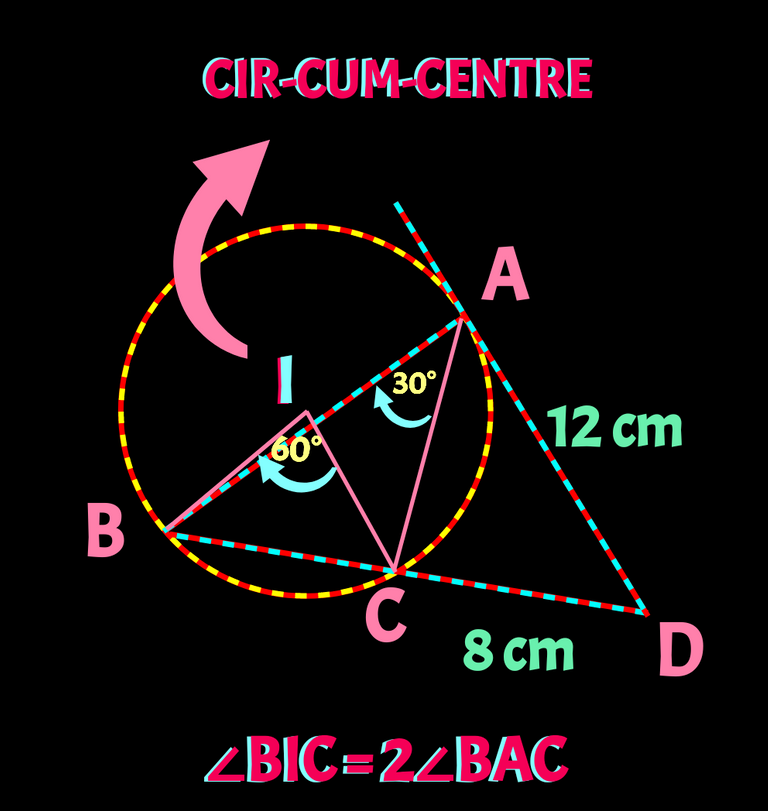
Now In ∆BIC side BI and CI are circumradious of the cricle. So, BI = CI and ∠BIC = 60°. Sum of other two triangle is also 120°. As mentioned in point 4️⃣,∠ IBC =∠ICB = 120°/2 = 60°. So, ∆BIC is a equlaterl triangle and hence three side are equal. So side BI = CI = BC.

now we need to find BC only which will Curcumradius (r).To find we gonna use the the formulla mentioned in point 1️⃣Check below👇

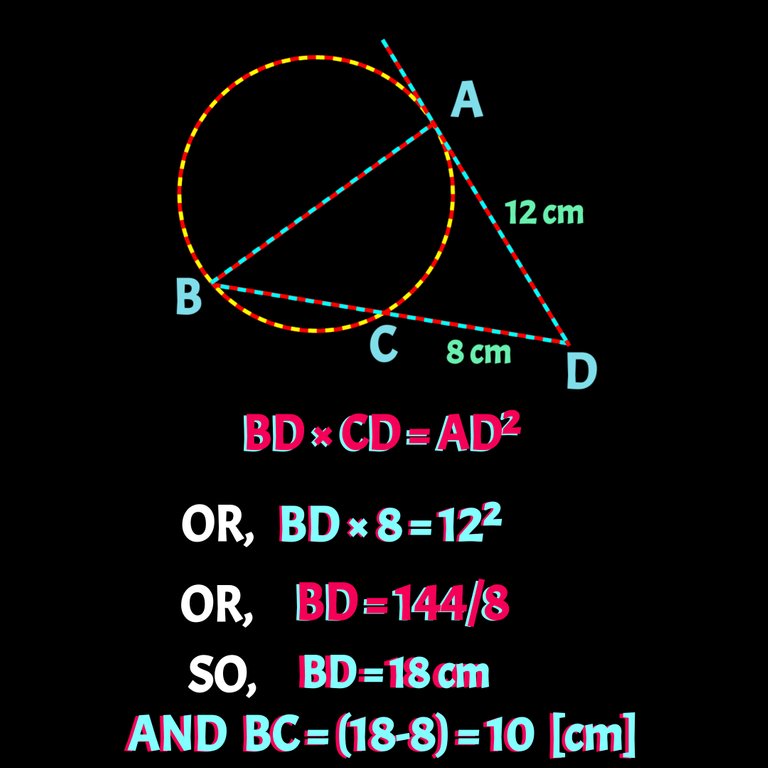
So we got radius. Now time for using point 5️⃣ to find Perimeter i.e perimeter of the cirlce is as follows:

All the figures are made by me using android apps. It takes time to build those figure; if you find any silly mistake ,please ignore it. Figures may not be accurate in measurement, just consider the data.

I hope you liked my today's work. Thank you so much for visiting.

Have a nice day

All is well

Regards: @meta007