Back to basics

Shout out to Math Only Math

In this article you will find:

• Introduction
• What is a matrix?
• Search for a value within an array
• Sum and remainder of matrices
• Matrix multiplication

Greetings to all!

I was thinking of doing a follow-up to my article on representing objects in space. For this, I planned to do a paper on representing the orientation of an object with rotation matrices.

However, I realized something with this method:

This falls heavily on understanding how matrices and angles work.

Likewise, if you've seen my previous posts in the Coding Basics series, we've used arrays to the max.

All this has led me to the conclusion that it would be illogical to advance my future articles if I do not first make a post on the basics of matrices. This is so that those Hive users who do not have knowledge of linear algebra can obtain a clearer concept of what matrices are.

For now we will focus on defining a matrix and basic operations with matrices, leaving more complex topics such as the inverse of a matrix and transposed matrices for another time.

Having said that,

Let's start!

What is a matrix?

Shoutout to Cuemath

According to the popular definition:

In mathematics, a matrix is a two-dimensional set of numbers.

But what does this mean?

Each number is an individual value, and in some cases we need to work with a large number of numbers to reach a conclusion. In this case we group them to form a set of numbers. This is precisely what a matrix is, a number of numbers organized in a single space.

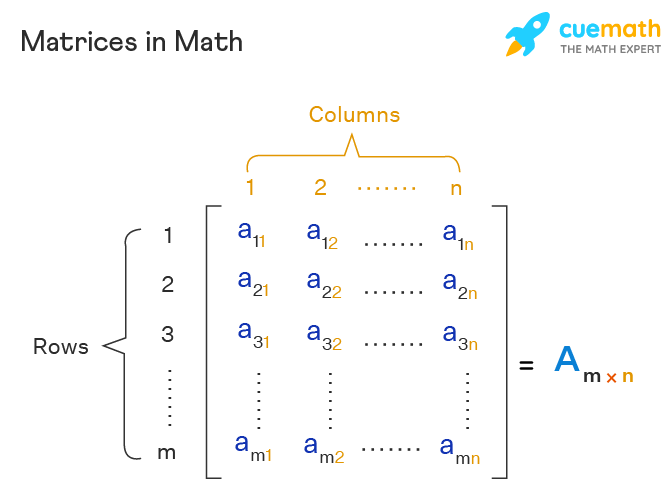
With respect to two-dimensional, tools that work with two parameters to recognize the position of a value can be called two-dimensional. In this case, these parameters are:

• Rows
• Columns

In this way, it can be said that a matrix is a set of numbers that are ordered by rows and columns. But what would the matrix look like?

A = [a11, a12, a13, ..., a1n]
    [a21, a22, a23, ..., a2n]
    [a31, a32, a33, ..., a3n]
    [... ... ... ... ... ...]
    [am1, am2, am3, ..., am4]

Here, we can see that the matrix is the letter A, whose content is observed on the other side of the equality, but we have not defined precisely how the perspective of rows and columns is used.

If we look at an example:

A = [0, 1, 2,  3 ]
    [4, 5, 6,  7 ]
    [8, 9, 10, 11]
    [12,13,14, 15]

In this example we have a 4x4 matrix, which is simply a matrix of 4 rows and 4 columns. We can check this by observing that the values of 0,1,2 and 3 form one row, those of 4,5,6 and 7 another, following this until we reach the last row which is formed by 12,13,14,15 and having 4 rows.

Although these values from left to right form a row, they can also form a column. To recognize a column, just count the numbers from top to bottom, starting with the values in the first row.

For example, if we look at the first column, we will see that it is formed by 0,4,8 and 12, the second by 1,5,9 and 13, which will be repeated until we reach the last column, formed by 3,7 ,11,15, thus having 4 columns

In this way, we can know that the matrix shown above has 4 rows and 4 columns, so we can say that it has 4x4 dimensions.

Note: Although each of the numbers or symbols in a matrix can be called elements, they can also be known as cells

Now that we know what a matrix is and how it works, we can look at some mathematical operations that we can perform with matrices.

Search for a value within an array

Shoutout to Wikipedia

If you are a programmer, you know that indexes are your bread and butter when searching for values in an array. But what are these indices based on?

When we create an array, which may be one-dimensional or two-dimensional as in the case of a matrix, each element, in addition to having a value, has a label that allows us to know what position it is in. If we take a one-dimensional array:

A1 = [1,2,3,4,5]

We can see the values of each element. However, when introduced into the array they will logically have a position value that we can call. If we look at this same arrangement in terms of position:

A1 = [position 0, position 1, position 2, position 3, position 4, position 5]

Which means that if we want to access value 3 of the array, we would have to go to position 3 of it.

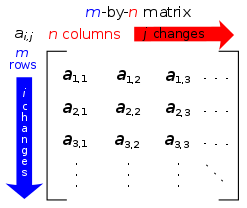
If we want to find a particular value according to its position in matrices, the only thing that changes is that the number of dimensions increases, that is, now in addition to searching for it by its row, we will also have to search for the element by its specific column. If we take an example:

A = [a11, a12, a13]
    [a21, a21, a23]
    [a31, a32, a33]

Here we can see that we have already identified the position of each element in its symbolic value. If we look at a21, this tells us according to the first number that it is in row 2, and the second number tells us that it is in column 1.

Translating this into a matrix that we would see in practice:

A = [1,2,3]
    [4,5,6]
    [7,8,9]

If we want to obtain the number found in row 2 and column 1, then we would go to the row where the values 4,5,6 are and at the same time to the column 1,4,7, knowing that the number that matches In these two analyzes it is four, which will be precisely the value in this position.

Addition and subtraction of matrices

Shoutout to Basic Mathematics

Let's start with the operations we can perform between two matrices. If we have a matrix A and a matrix B both with dimensions of 2x2:

A = [2,4]
    [6,8]

B = [1,3]
    [5,7]

So, if we wanted to add them, we would only have to add the elements of both that are in the same position. For example, if we add the elements found in row 1 and column 1, we would have 2 + 1 = 3. If we add those in row 2, column 1 we will have 4 + 3 = 7.

This process will be repeated until we obtain the following matrix, which we will call C:

C = [3, 7 ]
    [11,15]

Now, a misconception that we may have until now is that all matrices must be symmetrical (That is, they must always have the same number of columns and rows). However, this is not true, since you can have matrices of 2 x 3, 5 x 4, and any unequal dimension. For example, if we look at a 2x1 matrix:

A = [0]
    [1]

We can confirm this by seeing that A has two rows and one column.

However, something that will always have to be true for two matrices to be added is that both must have the same dimensions. For example, if we have a matrix A with 4x4 dimensions (4 rows and 4 columns), the matrix B with which it is added will also have to have 4x4 dimensions to be able to be added.

This will also be repeated for the subtraction of matrices, where the only thing that changes is that instead of adding, element by element is subtracted. If we subtract A from B from the previous example:

A = [2,4]
    [6,8]

B = [1,3]
    [5,7]

A - B = [1,1]
        [1,1]

Matrix Multiplication

Shoutout to Towards Data Science

Multiplying a matrix by an element follows the same rules that we understand about addition and subtraction, where we go element by element. If, for example, we have a matrix A and we want to multiply it by the number 2, we would have the following result:

A = [1,2]
    [3,4]

A*2

= [2,4]
  [6,8]

Where we see that 1 * 2 = 2, 2 * 2 = 4, repeating the process until we reach the last element.

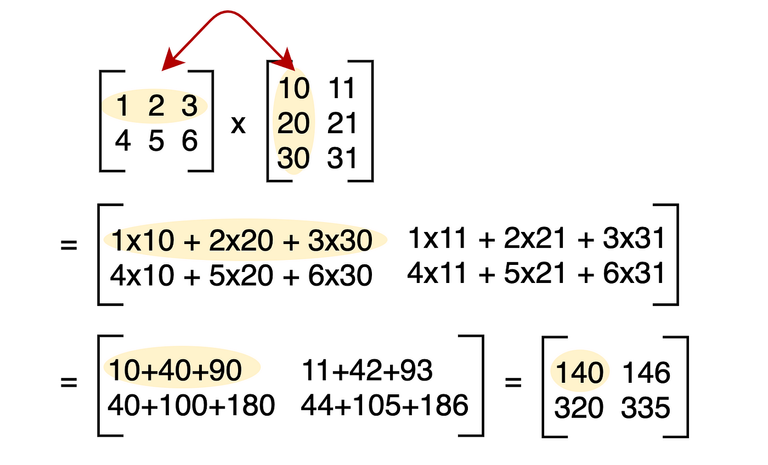
However, if we were to do a multiplication between two matrices, this process changes. Let's say we have two 3x3 matrices, one called A1 and another called A2:

A1 = [1,2,3]
     [4,5,6]
     [7,8,9]

A2 = [2, 4,  6]
     [8, 10, 12]
     [14,16, 18]

Now, if we multiply, we will have to do the following:

• Take the first element of a row and multiply it by the first element of a column of another row.
• Add the result of the first operation with the multiplication of the next element in the row of the first matrix by the next element in the column of the second matrix.
• Repeat this process until the last element in the row of the first matrix is reached. From the total sum, we would obtain the first element of the matrix A1*A2
• Iterate the procedure until you have all the values.

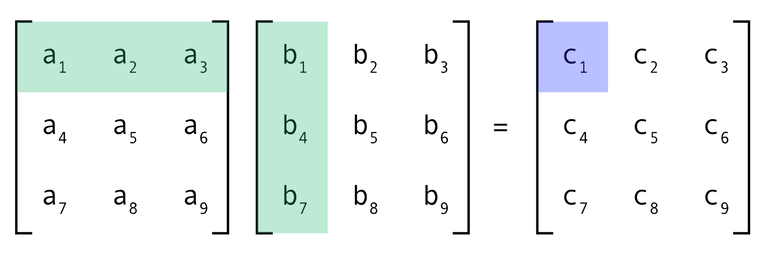
Shoutout to Charchithowitzer in Medium

If we look at it in a more practical way, performing the multiplication:

A1 * A2 = [(1*2)+ (2*8) + (3*14), (1*4) + (2*10) + (3*16), (1*6) + (2* 12) + (3*18)]
          [(4*2)+ (5*8) + (6*14),(4*4) + (5*10) + (6*16), (4*6) + (5*12) + ( 6*18)]
          [(7*2)+ (8*8) + (9*14),(7*4) + (8*10) + (9*16), (7*6) + (8*12) + ( 9*18)]

Solving the multiplications:

A1 * A2 = [2 + 16 + 42, 4 + 20 + 48, 6 + 24 + 54]
          [8 + 40 + 84,16 + 50 + 96, 24 + 60 + 108]
          [14+ 64 + 126,28 + 80 + 144, 42 + 96 + 162]

And finally, adding:

A1 * A2 = [60, 72, 84]
          [132,162,192]
          [204,252,300]

With which we would have our multiplication.

In addition to this, a condition that causes matrix multiplication to break the rule that the dimensions must be the same in both matrices is that if we have two matrices of different dimensions but the first one has the same number of columns that of rows the second, then it can be multiplied.

Let's see this with a simple example. If we have two matrices, one with dimensions 3x2 and another with dimensions 2x3, then we can multiply them, since matrix A has 2 columns and matrix B has 2 rows, which makes them coincide:

A = [0,1]
    [2,3]
    [4,5]

B = [1,2,3]
    [4,5,6]

Now, when multiplying these:

A * B = [(0*1) + (1*4), (0*2) + (1*5), (0*3) + (1*6)]
        [(2*1) + (3*4), (2*2) + (3*5), (2*3) + (3*6)]
        [(4*1) + (5*4), (4*2) + (5*5), (4*3) + (5*6)]

And when adding the results:

A*B = [4, 5, 6]
      [14,19,24]
      [24,33,42]

With which we will obtain that the dimensions of the resulting matrix will be precisely the number of rows of the first matrix and the number of columns of the second matrix (3x3).

I hope that this article has been able to explain clearly what matrices are and what we can do with them.

If you want to study a career in mathematics or a branch of engineering, you will see that the use of matrices will be your daily bread when you face some differential equations, numerical analysis problems, in computing and robotics.

This is why if you have any questions, just let me know and if you want to read more complex matrix concepts, comment if you want another edition.

Thank you very much for your support and good luck!

Volviendo a los principios

Shoutout to Math Only Math

En este artículo encontrarás:

• Introducción
• ¿Qué es una matriz?
• Buscar un valor dentro de una matriz
• Suma y resta de matrices
• Multiplicación de Matrices

¡Un saludo a todos!

Estaba pensando en realizar una continuación a mi artículo sobre la representación de objetos en el espacio. Para esto, planeaba realizar un artículo sobre la representación de la orientación de un objeto con matrices de rotación.

Sin embargo, me di cuenta de algo con este método:

Este recae de gran manera en el entendimiento de como funcionan las matrices y los ángulos.

De igual forma, si has visto mis posts previos en la serie de Coding Basics, hemos usado matrices a más no poder.

Todo esto me ha llevado a la conclusión de que sería ilógico avanzar en mis futuros artículos si primero no hago un post sobre lo básico de las matrices. Esto para que aquellos usuarios de Hive que no tengan conocimiento de álgebra lineal obtengan un concepto más claro de lo que son las matrices.

Por ahora nos enfocaremos en definir una matriz y las operaciones básicas con matrices, dejando tópicos más complejos como la inversa de una matriz y las matrices traspuestas para otra ocasión.

Dicho esto,

¡Comencemos!

¿Qué es una matriz?

Shoutout to Cuemath

Según la definición popular:

En matemática, una matriz es un conjunto bidimensional de números.

¿Pero que quiere decir esto?

Cada número es un valor individual, y en algunos casos necesitamos trabajar con una gran cantidad de números para llegar a una conclusión. En este caso los agrupamos para formar un conjunto de números. Esto es precisamente lo que es una matriz, una cantidad de números organizados en un solo espacio.

Con respecto a bidimensional, se puede llamar bidimensional a las herramientas que trabajan con dos parámetros para reconocer la posición de un valor. En este caso, estos parámetros son:

• Filas
• Columnas

De esta forma, se puede decir que una matriz es un conjunto de números que se encuentran ordenados por filas y columnas. Pero, ¿Cómo se vería la matriz?

A = [a11, a12, a13, ... , a1n ]
    [a21, a22, a23, ... , a2n ]
    [a31, a32, a33, ... , a3n ]
    [...  ...  ...  ...   ... ]
    [am1, am2, am3, ... , am4 ]

Aquí, podemos ver que la matriz es la letra A, cuyo contenido se observa al otro lado de la igualdad, pero no hemos definido precisamente como se usa la perspectiva de filas y columnas.

Si observaramos un ejemplo:

A = [0, 1, 2,  3 ]
    [4, 5, 6,  7 ]
    [8, 9, 10, 11]
    [12,13,14, 15]

En este ejemplo tenemos una matriz 4x4, que es simplemente una matriz de 4 filas y 4 columnas. Esto lo podemos comprobar observando que los valores de 0,1,2 y 3 forman una fila, los de 4,5,6 y 7 a otra siguiendo esto hasta llegar a la última fila que está formada por 12,13,14,15 y teniendo 4 filas.

Si bien estos valores de izquierda a derecha forman una fila, también pueden formar columna. Para reconocer una columna, solo basta con contar los números de arriba hacia abajo, comenzando por los valores de la primera fila.

Por ejemplo, si observamos la primera columna, veremos que esta está formada por 0,4,8 y 12, la segunda por 1,5,9 y 13, lo cual se repetirá hasta llegar a la última columna, formada por 3,7,11,15, teniendo así 4 columnas

De esta forma, podemos saber que la matriz mostrada anteriormente tiene 4 filas y 4 columnas, con lo que podemos decir que tiene 4x4 dimensiones.

Nota: Si bien cada uno de los números o símbolos en una matriz pueden llamarse elementos, de igual manera pueden ser conocidos como celdas

Ahora que sabemos qué es una matriz y como funciona, podemos observar algunas operaciones matemáticas que podemos realizar con matrices.

Buscar un valor dentro de una matriz

Shoutout to Wikipedia

Si eres un programador, sabrás que los índices son el pan de cada día al buscar valores es un arreglo. Pero, ¿En que se basan estos índices?

Cuando creamos un arreglo, que bien puede ser de una dimensión o dos dimensiones como el caso de una matriz, cada elemento, además de tener un valor, tiene una etiqueta que nos permite saber en que posición está. Si tomamos un arreglo de una dimensión:

A1 = [1,2,3,4,5]

Podemos ver los valores de cada elemento. Sin embargo, al ser introducidos en el arreglo lógicamente tendrán un valor de posición que podremos llamar. Si observamos este mismo arreglo en términos de posición:

A1 = [posición 0, posición 1, posición 2, posición 3, posición 4, posición 5]

Lo que significa que si queremos acceder al valor 3 del arreglo, tendríamos que dirigirnos a la posición 3 de este.

Si queremos encontrar un valor en particular según su posición en matrices, lo único que cambia es que aumenta el número de dimensiones, es decir, que ahora además de buscarlo por su fila, tendremos que buscar también al elemento por su columna específica. Si tomamos un ejemplo:

A = [a11, a12, a13]
    [a21, a21, a23]
    [a31, a32, a33]

Aquí podemos ver que ya tenemos identificado la posición de cada elemento en su valor simbólico. Si observamos a21, este nos indica según el primer número que está en la fila 2, y el segundo número nos indica que está en la columna 1.

Traduciendo esto a una matriz que veríamos en la práctica:

A = [1,2,3]
    [4,5,6]
    [7,8,9]

Si queremos obtener el número que se encuentra en la fila 2 y columna 1, entonces nos dirigiríamos a la fila donde están los valores 4,5,6 y al mismo tiempo a la columna 1,4,7, sabiendo que el número que coincide en estos dos análisis es el cuatro, que será justamente el valor en esta posición.

Suma y resta de matrices

Shoutout to Basic Mathematics

Comencemos con las operaciones que podemos realizar entre dos matrices. Si tenemos una matriz A y una matriz B ambas con dimensiones de 2x2:

A = [2,4]
    [6,8]
    
B = [1,3]
    [5,7]

Entonces, si quisieramos sumarlas, solamente, tendríamos que sumar los elementos de ambas que se encuentren en la misma posición. Por ejemplo, si sumamos los elementos que se encuentran en la fila 1 y columna 1, tendríamos 2 + 1 = 3. Si sumamos los de la fila 2, columna 1 tendremos 4 + 3 = 7.

Este proceso se repetirá hasta obtener la siguiente matriz, a la que llamaremos C:

C = [3, 7 ]
    [11,15]

Ahora, una idea equivocada que podemos tener hasta ahora es que todas las matrices deben ser simétricas (Es decir, que siempre se deba tener el mismo número de columnas y de filas). Sin embargo, esto no es cierto, puesto que se pueden tener matrices de 2 x 3, 5 x 4 y cualquier dimensión desigual. Por ejemplo, si observamos una matriz de 2x1:

A = [0]
    [1]

Podemos confirmarlo al ver que A tiene dos filas y una columna.

Sin embargo, algo que siempre tendrá que cumplirse para que dos matrices puedan sumarse es que ambas deben tener las mismas dimensiones. Por ejemplo, si tenemos una matriz A con 4x4 dimensiones (4 filas y 4 columnas), la matriz B con la que se sume tendrá que tener igualmente 4x4 dimensiones para poder sumarse.

Esto también se repetirá para la resta de matrices, donde lo único que cambia es que en vez de sumar, se resta elemento a elemento. Si restamos A con B del ejemplo anterior:

A = [2,4]
    [6,8]
    
B = [1,3]
    [5,7]
    
A - B = [1,1]
        [1,1]

Multiplicación de Matrices

Shoutout to Towards Data Science

El multiplicar una matriz por un elemento sigue las mismas reglas que entendemos de la suma y resta, donde vamos elemento por elemento. Si por ejemplo, tenemos una matriz A y queremos multiplicarla por el número 2, tendríamos el siguiente resultado:

A = [1,2]
    [3,4]
    
A * 2

= [2,4]
  [6,8]

Donde vemos que 1 * 2 = 2, 2 * 2 = 4, repitiendo el proceso hasta llegar al último elemento.

Sin embargo, si hicieramos una multiplicación entre dos matrices, este proceso cambia. Digamos que tenemos dos matrices 3x3, una llamada A1 y otra llamada A2:

A1 = [1,2,3]
     [4,5,6]
     [7,8,9]
     
A2 = [2, 4,  6 ]
     [8, 10, 12]
     [14,16, 18]

Ahora, si multiplicamos, tendremos que hacer lo siguiente:

• Tomar el primer elemento de una fila y multiplicarlo por el primer elemento de una columna de otra fila.
• Sumar el resultado de la primera operación con la multiplicación del siguiente elemento en la fila de la primera matriz por el siguiente elemento de la columna de la segunda matriz.
• Repetir este proceso hasta que se llegue al último elemento de la fila de la primera matriz. De la suma total, obtendríamos el primer elemento de la matriz A1*A2
• Iterar el procedimiento hasta tener todos los valores.

Shoutout to Charchithowitzer in Medium

Si lo observamos de una forma más práctica, realizando la multiplicación:

A1 * A2 = [(1*2)+ (2*8) + (3*14), (1*4) + (2*10) + (3*16), (1*6) + (2*12) + (3*18)]
          [(4*2)+ (5*8) + (6*14),(4*4) + (5*10) + (6*16), (4*6) + (5*12) + (6*18)]
          [(7*2)+ (8*8) + (9*14),(7*4) + (8*10) + (9*16), (7*6) + (8*12) + (9*18)]

Resolviendo las multiplicaciones:

A1 * A2 = [2 + 16 + 42, 4 + 20 + 48, 6 + 24 + 54]
          [8 + 40 + 84,16 + 50 + 96, 24 + 60 + 108]
          [14+ 64 + 126,28 + 80 + 144, 42 + 96 + 162]

Y finalmente, sumando:

A1 * A2 = [60, 72, 84]
          [132,162,192]
          [204,252,300]

Con lo que tendríamos nuestra multiplicación.

Además de esto, una condición que hace que la multiplicación de matrices pueda romper la regla de que las dimensiones deban ser las mismas en ambas matrices, es la de que si tenemos dos matrices de diferentes dimensiones pero que la primera tiene el mismo número de columnas que de filas la segunda, entonces se puede multiplicar.

Veamos esto con un ejemplo sencillo. Si tenemos dos matrices, una de dimensiones 3x2 y otra de dimensiones 2x3, entonces podemos multiplicarlas, ya que matriz A tiene 2 columnas y matriz B tiene 2 filas, lo que hace que coincidan:

A = [0,1]
    [2,3]
    [4,5]

B = [1,2,3]
    [4,5,6]

Ahora, al multiplicar estas:

A * B = [(0*1) + (1*4), (0*2) + (1*5), (0*3) + (1*6)]
        [(2*1) + (3*4), (2*2) + (3*5), (2*3) + (3*6)]
        [(4*1) + (5*4), (4*2) + (5*5), (4*3) + (5*6)]

Y al sumar los resultados:

A * B = [4, 5, 6 ]
        [14,19,24]
        [24,33,42]

Con lo que obtendremos que las dimensiones de la matriz resultante serán precisamente el número de filas de la primera matriz y el número de columnas de la segunda matriz (3x3).

Espero que este artículo haya podido explicar de manera clara que son las matrices y que podemos hacer con estas.

Si deseas estudiar una carrera en matemáticas o una rama de la ingeniería, verás que el uso de matrices será el pan de cada día cuando te enfrentes a algunas ecuaciones diferenciales, problemas de análisis numérico, en la informática y la robótica.

Es por esto que si tienes alguna duda, solo dejamelo saber y si quieres leer conceptos más complejos de matrices, comenta si quieres otra edición.

¡Muchas gracias por tu apoyo y buena suerte!