Distribución de esfuerzos en el suelo y su variación con la profundidad: abordaje del MÉTODO FADUM para el caso de carga lineal idealizada con situaciones de la vida real

over 1 year ago (Edited)

Esta entrega viene hacer la continuación del trabajo titulado “Ingeniería con creatividad: iniciación al estudio de la variación con la profundidad de las presiones en el suelo”, entrega donde se abordaron las hipótesis que como especialistas en suelos para fines de ingeniería civil, nos orientan para idealizarlo como una masa homogénea, elástica y semi - infinita. A través de la teoría de BOUSSINESQ abordamos el caso de una carga puntual, la cual puede estar representada por la carga que transmite una columna de un edificio, o un poste de esos que se utilizan en las redes de electricidad de una urbanización. Pero ¿qué sucede cuando el problema ya no es una carga puntualizada, sino que se trata de una carga que se distribuye a lo largo de una determinada longitud? Y es allí donde entra la solución de FADUM, que viene siendo como una extensión de la teoría de BOUSSINESQ.

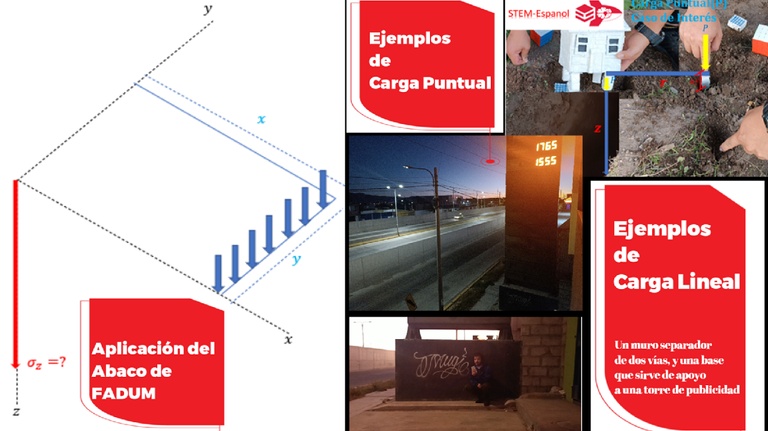
En ese sentido, surgen diversos objetivos específicos que se desean lograr con esta publicación, que vayan en pro de: comprender el proceso de distribución de presiones con la profundidad en una masa de suelo, como consecuencia de la aplicación de una carga lineal. Vale destacar que cada uno de estos objetivos estructuran el cuerpo de esta publicación, y los mismos se señalan a continuación:

01.- Estudiar la extensión de la ecuación de Boussinesq y el aporte de Fadum para la solución matemática del problema de carga lineal

02.-Definir el problema de carga lineal con una situación de la vida real

03.- Identificar las variables para la estimación del factor de influencia de FADUM

04.- Desarrollar ejemplos prácticos

Espero se disfruten de esta publicación, preparada con mucho cariño para la comunidad de StemSocial, la sub-comunidad de Stem-Espanol, y todos los amantes de la ciencia que hacemos vida en la fascinante blockchain de HIVE. Procedamos ahora a desarrollar cada uno de estos objetivos planteados.

Estudio de la extensión de la ecuación de Boussinesq y el aporte de Fadum para la solución matemática del problema de carga lineal

Una forma resumida de presentar la ecuación de Boussinesq definida en el año 1865, es la que se expresa a continuación:

Eta ecuación solo funciona para el caso de carga puntual, y en la referencia 03 fue abordada, por lo que te recomendamos la lectura de la misma. Ahora bien, el aporte de las MATEMÁTICAS a simple vista se ve reflejado en el proceso de extender esta solución para el caso de carga lineal, a través de técnicas de integración cuyo abordaje se escapa del alcance de esta publicación, y que dan como resultado la siguiente expresión:

Noten que en esta extensión de la ecuación 01 el término “P” ahora aparece en minúscula, y esto es para hacer la distinción de que esta expresión está dirigida al caso de carga lineal. Ahora bien, la ecuación 02 se puede simplificar para un mejor manejo, incluyendo valores adimensionales que vienen del cociente de los valores de distancia “x” “y” por la profundidad de estudio “z”, es decir:

Obteniendo así la siguiente expresión:

Una ecuación que a pesar de la inclusión de estos factores adimensionales, se sigue viendo complicada, pero tranquilos, que afortunadamente investigadores del siglo XX trabajaron fuertemente para hacer más fácil el proceso de cálculo al ingeniero especializado en suelos, en este sentido, todo esto resaltado en color verdad en la ecuación 05, simplemente se denomina factor de influencia “po”, obteniendo una ecuación bastante sencilla, como la que sigue a continuación:

Y en torno a este término resaltado en color “amarillo” FADUM plantea como solución práctica el uso de un ábaco, del cual de manera didáctica dibujaré las principales características, para que en líneas generales conozcas los conceptos que el uso de este ábaco involucra, aspecto esencial para la solución del problema de distribución de presiones en el suelo por carga lineal:

Vale destacar que esto corresponde a una ilustración didáctica al ábaco de FADUM, en la referencia 02 lo podrás encontrar con total exactitud, aquí simplemente te presento de forma didáctica los diversos elementos que lo constituyen, para comprender el manejo de la información hasta llegar a “po”. Esto último es bastante sencillo, simplemente necesitamos conocer “y”, variable que corresponde a la longitud de la carga lineal, “x” la distancia de esta carga con respecto al punto donde deseamos estimar la variación con la profundidad del esfuerzo producido por dicha carga “σz y "z" que es la profundidad de interés. Conociendo cada una de estas variables, obtenemos el valor de "n" para entrar al ábaco por el eje de las abscisas, luego proyectamos una linea perpendicular a este eje, hasta cortar la curva de "m" valores, y de allí se traza una horizontal que corte al eje de las ordenadas, y obtener así Po.

La tabla que se presenta corresponde a valores reales del Ábaco de FADUM aplicando los pasos anteriormente descritos. Estos valores se han seleccionado estratégicamente, dado que los estaremos utilizándolos en los ejemplos prácticos.

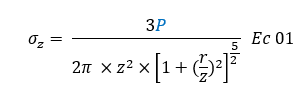
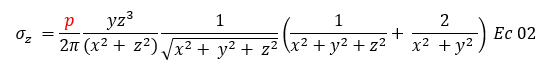
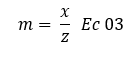
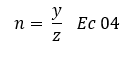
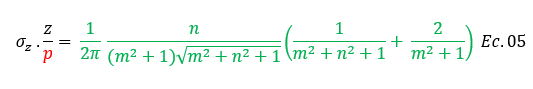
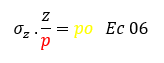
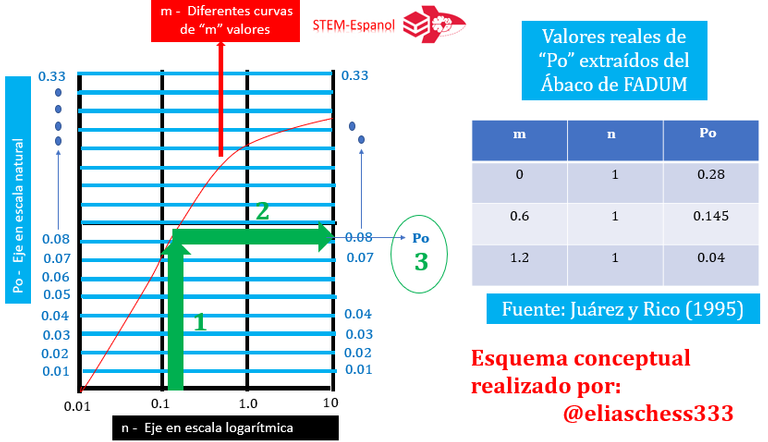
Definición del problema de carga lineal con una situación de la vida real

Como profesor de Mecánica de Suelos, veo la necesidad de llevar los conocimientos difundidos y debatidos en clases a la vida real, esto es importante para que el estudiante de esta asignatura de la ingeniería civil afiance de la mejor manera los conocimientos impartidos. Es así como bajo la tónica de “Educar más allá de los muros del aula”, en uno de mis paseos por la hermosa ciudad de Arequipa, me detuve para tomar una captura de la base usada para una gran publicidad a una estación de servicio. Esta base ilustra bastante bien una carga lineal que es trasmitida al suelo, con una longitud aproximada de 2. 5 metros.

Otro ejemplo de carga lineal corresponde a este gran muro que divide la vía en una autopista principal, y en una avenida secundaria para el tránsito vehicular a baja velocidad, donde los vehículos puedan estacionarse para llegar a los diferentes comercios que se encuentran de ese lado.

A continuación comparto una vista de estos dos ejemplos, donde podemos apreciar de mejor manera la publicidad de la estación de servicio, y como esta se apoya en una gran base:

Estos casos presentados en cada una de esta imágenes los podemos clasificar como carga lineal, cuyas unidades típicas son de fuerza dividida por longitud, como por ejemplo “Ton/m”. Este tipo de carga lo podemos presenciar también en edificaciones, como por ejemplo en una viga de cimentación que le sirve de base a un muro de mampostería, en donde el conjunto fundación - muro transmite una carga que se puede idealizar como un carga lineal al suelo de fundación, siendo de interés saber cómo esta carga se distribuye con la profundidad, para lo cual es necesario identificar las variables "x" "y" "z", para hacer uso del ábaco de FADUM, esto se aborda en el tópico que sigue.

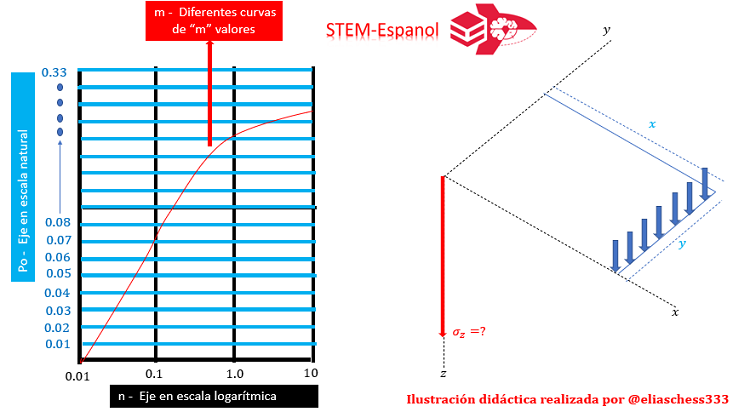
Identificación de las variables para la estimación del factor de influencia de FADUM

Una vez identificado el caso de carga, siendo para el presente estudio carga lineal, el reto es representar las variables “x” “y” z” en el mismo, para el caso de la base que sirve de soporte a la valla publicitaria se tiene lo siguiente:

Tal como se explicó en párrafos anteriores, “y” es la longitud de esta carga lineal, por otro lado “x” es la distancia del punto a donde quiero determinar el esfuerzo “σz” y su variación con la profundidad. La variable “x” puede ser cero, si es que quiero determinar este valor de esfuerzo justo en el extremo de la carga idealizada como lineal. Para el caso del muro en la vialidad se tiene lo siguiente:

Digamos que es el mismo principio que el caso anterior, con la salvedad de que en el ábaco de FADUM los valores de “n” condicionan la longitud de la carga lineal, en ese sentido, es necesario dividir este muro en varios tramos, obviamente es importante que la construcción del muro también existan juntas de separación entre los diversos tramos, , de forma que coincida en la medida de lo posible la forma como estos fueron analizados con el proceso constructivo. Considero que es oportuno resolver algunos ejemplos prácticos, con la intención de que estos resultados nos lleven a realizar las respectivas conclusiones de este fascinante estudio.

Desarrollo de ejemplos prácticos

Antes de iniciar con los ejemplos de la ecuación 06 procedamos a despejar la variable asociada a los esfuerzos, obteniendo la siguiente ecuación:

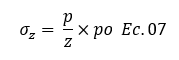
Vamos a estar realizando tres ejemplos en los que se mantiene la longitud de la carga lineal, es decir, y= 5m, se mantiene la profundidad de interés z= 5m, y el valor de la carga para fines didácticos supondremos que es de 12 T/m; pero variamos los valores de x, para los casos de x= 0, x= 3m , x= 6m. Resolvamos el caso número 01:

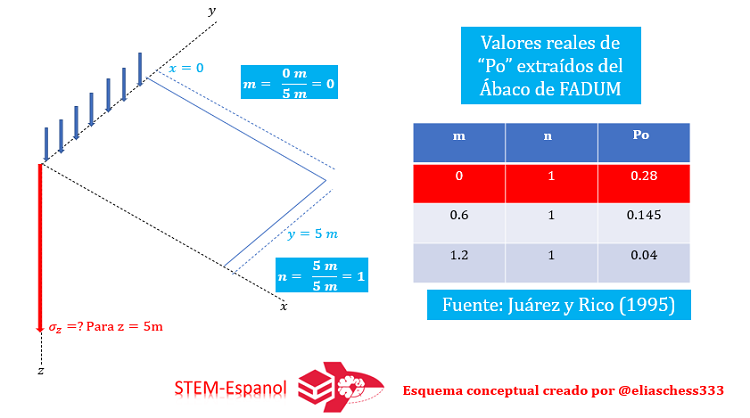
Sustituimos en la ecualicen 07:

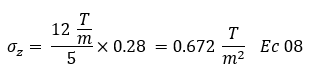
En cuanto al caso 02 tenemos:

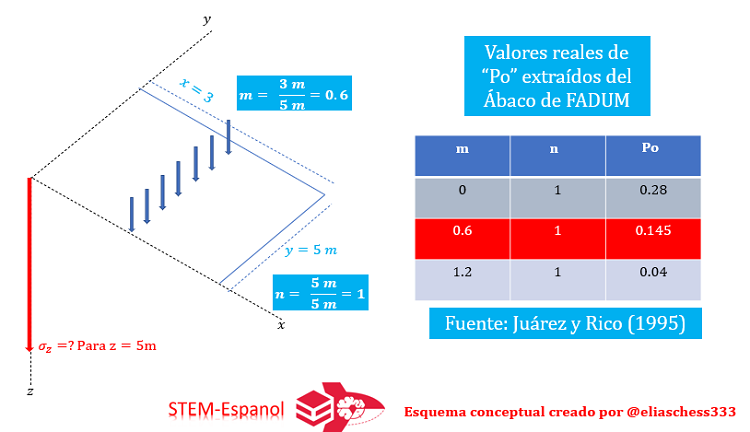
Al sustituir en la ecuación el valor de esfuerzo a la profundidad de 5m es:

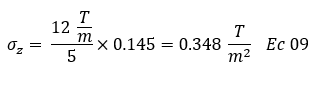
Finalmente, para el caso 03:

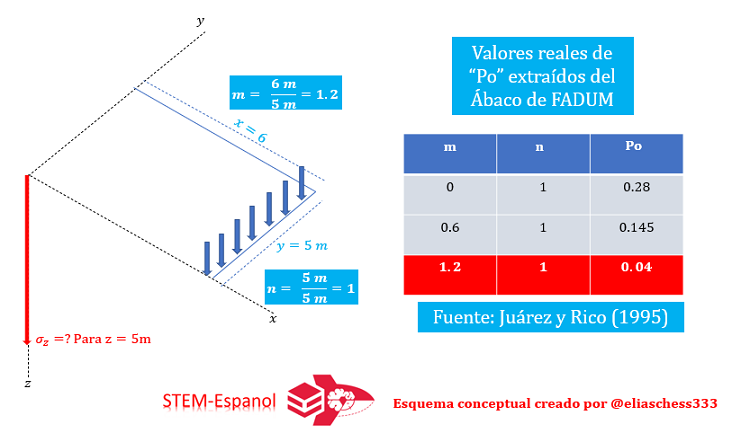
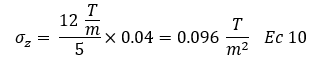
Conclusiones

Contento de haber abordado un caso más del problema de la distribución de presiones con la profundidad, espero este material sea de utilidad a estudiantes de la carrera ingeniería civil, o profesionales cuya línea de trabajo esté vinculada a la geotecnia y mecánica de suelos. También espero que este material llegue a lectores que si bien no son ingenieros o estudiantes de esta carrera, disfruten del recorrido didáctico que se hace, y con las imágenes reales entiendan a groso modo este problema de la distribución de presiones con la profundidad. Las conclusiones de mayor relevancia son las siguientes:

01.- En la medida que nos alejamos del punto de aplicación de la carga, los esfuerzo en la masa del suelo a una profundidad determinada van disminuyendo.

02.-El ábaco de FADUM es limitado para el caso de cargas líneas de gran longitud, simplificar los problemas para ajustarlos a la herramienta de trabajo puede ser una solución.

03.-Todos estos aportes realizados parten de la premisa de ver al suelo como un material homogéneo, isotrópico y semi - infinito.

Espero todos los contenidos expuestos hayan sido de su agrado. Nos leemos y escuchamos en una próxima oportunidad. Escribió para ustedes:

@eliaschess333

Fuentes de información consultadas

01.- Eulalio Juarez y Alfonzo Rico. Mecánica de Suelos, Tomo 1: fundamentos de la Mecánica de Suelos. Editorial Limusa. Año: 1995

02.- Eulalio Juarez y Alfonzo Rico. Mecánica de Suelos, Tomo 2: teoría y aplicaciones de la Mecánica de Suelos. Editorial Limusa. Año: 1995

Lecturas recomendadas.

03.- Ingeniería con creatividad: iniciación al estudio de la variación con la profundidad de las presiones en el suelo. Disponible en: https://hive.blog/hive-196387/@eliaschess333/tbiqrsqw

Créditos	Credits
@eliaschess333 - Autor de la Publicación	@eliaschess333- Publication Author
Todas las fotografías son propiedad del autor, editadas en los casos que fue necesario con las herramientas PAINT, POWERPOINT, FILMORA 11	All photographs are property of the author, edited where necessary with the tools PAINT, POWERPOINT, FILMORA 11.
Los logos empleados de redes sociales son de uso libre, a continuación los enlaces: Instagram Youtube Twitter TikTok Facebook	The logos used in social networks are free to use, here are the links: Instagram Youtube Twitter TikTok Facebook