Lógica Combinacional - Operaciones lógicas básicas

Aunque suena un poco contradictorio pienso que las primeras programaciones en un lenguaje se hicieron sin escribir códigos o instrucciones en un software, de hecho algunos lenguajes de programación están basados en lógicas de control por hardware.

Para aclarar esto que puede sonar un poco confuso hoy me gustaría presentar la lógica combinacional basada en dispositivos o componentes electrónicos.

Estos componentes pueden combinarse entre sí para crear una lógica de control en la cual las salidas se activaran solo cuando la combinación de las entradas sea la requerida, de ahí su nombre de lógica combinacional y aunque parece algo simple es mucho lo que se puede controlar.

Pixabay

Es importante tener en cuenta todo lo aprendido en temas anteriores y para efectos de este tipo de lógica no tomamos en cuenta la magnitud física e una variable (resistencia, corriente, voltaje, otras) sino que, simplemente entendemos que un valor lo suficientemente alto para activar o una señal que indica activado se representa con un 1 y en caso contrario se representa con un 0.

Ahora repasamos un poco lo que son entradas y salidas.

• Entradas: Todos aquellos valores que pueden ser leídos, estos pueden provenir de interruptores, suiches, conmutadores, contactores, relés o similares. Estas pueden ser discretas cuando solo toman dos valores en el tiempo los cuales en nuestro caso estan representados como 1 y 0, y analogicas cuando toman diferentes valores en el tiempo dentro de un rango finito, las señales analógicas no aplicarán en nuestro artículo sobre lógica combinacional por razones obvias.

• Salidas: Son aquellos valores que pueden escribir o enviar instrucciones para el accionamiento de un dispositivo que generalmente es una luz, motor, pantalla, altavoz, o similares. También pueden ser análogicas o discretas, pero en nuestro caso solo tomaremos en cuenta las discretas.

En algunas ocasiones una salida puede ser usada como entrada a un operador, esto es común en los diagramas de control de lazo cerrado donde se monitorea la salida para garantizar la operación, también lo veremos en elementos de lógica combinacional donde una combinación de salidas se combierten en una combinación de entradas a otros operandos.

Ahora veamos algunas operaciones lógicas básicas que podemos "armar" en un circuito para aplicar lógica combinacional.

1. Suma Lógica: También se conoce como or que podemos leer en nuestro idioma como o,es decir, una cosa o alguna otra. Lo que hace este operando es que establece una condición en la que se evaluan las entradas y la salida solo se activara (será 1) si esta activa una de las entradas. Hagamos un circuito de ejemplo:

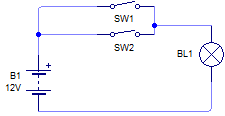
Circuito ejemplo de operador or, fuente: el autor

Vemos una lampara BL1 que representa una salida y dos interruptores SW1 y SW2 que representan cada uno una entrada, podríamos decir que tenemos un operador or de dos entradas en cuyo caso la salida se activará si se acciona SW1 ó SW2, note que el operador solo toma en cuenta que una de ambas entradas esté activa por lo que la condición de ambas entradas activas entra dentro de este parámetro.

Lo que establece un operador or es que una salida se active cuando al menos una de sus entradas sea 1, no está limitado a dos entradas pudiendo ser muchas inclusive. Un ejemplo práctico sería una alarma de casa donde se colocarían sensores de apretura en todas las puertas y ventanas bastando que solo una de ellas se active para activar la alarma.

Existe un componente electrónico para el diseño de circuitos de lógica combinacional que cumple con la función or, internamente está compuesto por muchos transistores pero basados en su operación se representan con un símbolo propio y recibe el nombre de compuerta lógica or 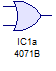generalmente estos vienen en un encapsulado que contiene 4 o más compuertas en él y pueden ser de tecnología CMOS o TTL.

Cuando se diseñan este tipo de circuitos se deben considerar todas las combinaciones y no solo aquellas que son de nuestro interés, es así porque se debe crear un circuito cuya lógica esté preparada para todas las posibilidades sin incumplir su funcionamiento.

Esto se logra con la llamada "tabla de la verdad", en la tabla de la verdad se toman en cuenta todas las entradas y sus combinaciones, luego según el criterio de control se establecen para cuales combinaciones de las entradas las salidas se activaran y luego de esto se procede con el diseño.

La tabla de la verdad para el operador or es la siguiente:

A	B	C (A+B)
0	0	0
0	1	1
1	0	1
1	1	1

Tabla de la verdad para la operación OR (C=A+B)

Si establecemos que A y B son entradas y C representa la salida de una combinación OR de A y B para números binarios entonces podemos saber cuales combinaciones de entradas producirán una activación de salida.

1. Producto lógico: Para que la salida sea 1 el producto de todas las entradas debe ser 1, visto desde un punto de vista lógico sabemos que esto no será posible si al menos una de las entradas es 0 porque hará que el resultado sea 0 de lo cual simplificamos en decir que la salida será 1 si y solo si todas las entradas son 1 por eso tambien recibe el nombre de AND, ilustremos esto con un circuito sencillo.

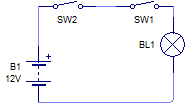
Circuito ejemplo de operador AND, fuente: el autor

Ahora si queremos encender BL1 no basta con accionar un solo SW, se deben accionar SW1 y SW2, de lo contrario BL1 no encenderá. Al igual que una OR existen componentes integrados que presentan compuertás lógicas AND, el símbolo para diseñar con AND es 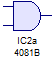y también pueden tener más de dos entradas, su tabla de la verdad es:

A	B	C (AxB)
0	0	0
0	1	0
1	0	0
1	1	1

Tabla de la verdad para la operación AND (C=AxB)

1. Negación Lógica: Este operador lo que hace es presentar una salida con un valor opuesto a la entrada, si una entrada es 1 su salida sera 0 y viceversa.

Para ilustrar este operador me apoyaré en el circuito presentado durante el artículo Transistor BJT Como conmutador

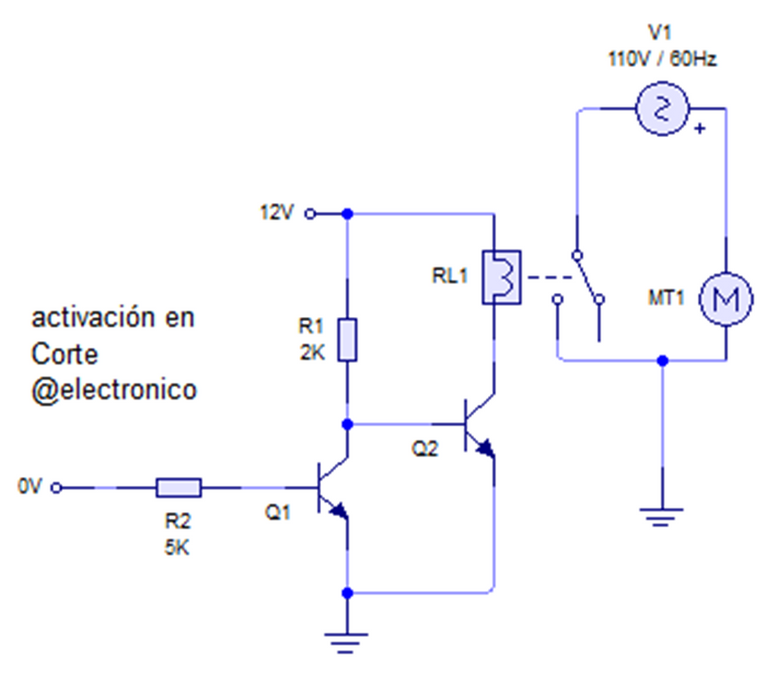
De lo aprendido en aquel artículo podemos recordar que la salida de Q2 es una negación de la entrada de Q1 porque cuando la base de Q1 es 0 el voltaje de colector aparece en la base de Q2 haciendo que su salida sea 1, entonces si entrada es 1 Salida es 0 y si entrada es 0 salida es 1 ilustrando perfectamente el comportamiento de una Negación lógica.

El elemento que representa la negación lógica se llama también compuerta NOT y es representada con el símbolo 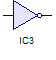se puede notar que tiene solo una salida y una entrada porque su función es negar un valor, su tabla de la verdad es:

A	A´
0	1
1	0

Tabla de la verdad para la operación NOT (A=A') A' se lee como A negada

Estos son los operadores básicos pero no los únicos, se pueden combinar sus lógicas para dar forma a otras compuertas lógicas si por ejemplo colo camos una NOT a la salida de una AND obtenemos una NAND 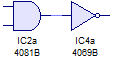pero como esta compuerta existe en circuitos integrados goza de su propio símbolo como operador lógico .

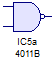De la misma forma se existe la NOR 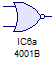que es una OR negada.

Otras son llamadas compuertas exclusivas como la OR exclusiva o XOR 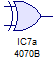cuya salida sera 1 solo cuando una de sus entradas sea 1, a diferencia de la OR si sus dos entradas son 1 su salida es 0, así que solo una de sus entradas debe estar activa para poder activarse.

Por supuesto también existe en su versión negada como NOR exclusiva o XNOR a es igual a la NOR pero cuando ambas entradas son 0 su salida es 0, de manera que solo será 1 cuando solo una de sus entradas sea 0.

Considero que este material es suficiente para cubrir una amplia introducción a la lógica combinacional, así que por ahora me despido pero no sin antes agradecerte por haberte tomado el tiempo de leer mi artículo, quedo atento a tus comentarios.

Lecturas recomendadas

• Ronald J. Tocci, Neal S. Widmer, Sistemas digitales: principios y aplicaciones
• Albert Paul Malvino, Principios de electrónica, Sexta edición.
• Robert L. Boylestad, Electrónica: Teoría de Circuitos.
• Timothy J. Maloney, Electrónica Industrial, dispositivos y sistemas.